题目内容
(本小题满分12分)
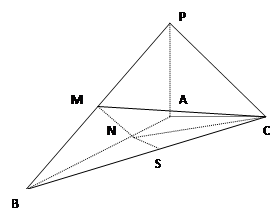
如图,已知三棱锥P=ABC中,PA⊥PC,D为AB的中点,M为PB的中点,且AB=2PD.
(1)求证:DM//面PAC;
(2)找出三棱锥P—ABC中一组面与面垂直的位置关系,并给出证明(只需找到一组即可).
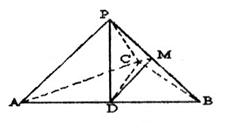
如图,已知三棱锥P=ABC中,PA⊥PC,D为AB的中点,M为PB的中点,且AB=2PD.
(1)求证:DM//面PAC;
(2)找出三棱锥P—ABC中一组面与面垂直的位置关系,并给出证明(只需找到一组即可).

(1)证明:依题意D为AB的中点,M为PB的中点
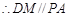 …………1分
…………1分
又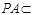 平面
平面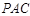 ,
,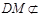 平面
平面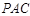
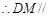 面
面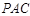 …………4分
…………4分
(2)平面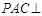 平面
平面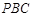 …………5分
…………5分
证明:由已知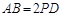 ,又D为AB的中点
,又D为AB的中点
所以PD=BD,又知M为PB的中点
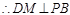 …………8分
…………8分
由(1)知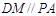
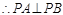 …………9分
…………9分
又由已知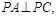 且
且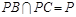
故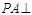 平面
平面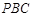 ,又
,又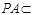 平面
平面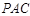
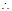 平面
平面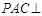 平面
平面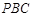
 …………12分
…………12分
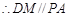 …………1分
…………1分又
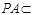 平面
平面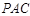 ,
,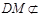 平面
平面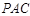
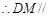 面
面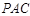 …………4分
…………4分(2)平面
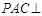 平面
平面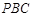 …………5分
…………5分证明:由已知
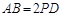 ,又D为AB的中点
,又D为AB的中点所以PD=BD,又知M为PB的中点
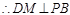 …………8分
…………8分由(1)知
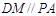
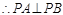 …………9分
…………9分又由已知
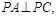 且
且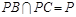
故
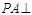 平面
平面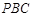 ,又
,又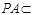 平面
平面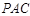
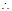 平面
平面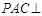 平面
平面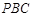
 …………12分
…………12分略

练习册系列答案
相关题目
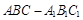 的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设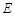 为线段
为线段 上的点.
上的点. 的体积;
的体积; 平面
平面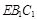 ,若存在,求AE的长.
,若存在,求AE的长.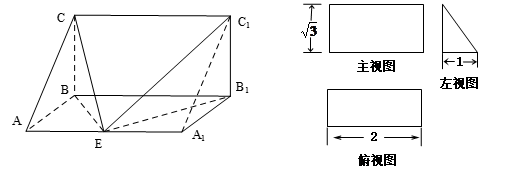
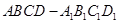 的棱长为2,
的棱长为2,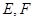 分别是
分别是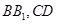 的中点.
的中点.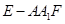 的体积;
的体积;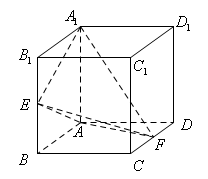
 —
— 的底面边长为
的底面边长为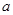 ,侧棱长为
,侧棱长为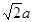 ,则
,则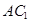 与侧面
与侧面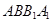 所成的角为( )
所成的角为( )
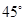

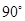
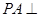 平面
平面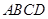 ,四边形
,四边形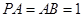 ,
,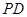 与平面
与平面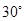 ,点
,点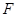 是
是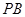 的中点,点
的中点,点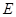 在矩形
在矩形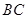 上移动.
上移动.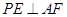 ;
; 等于何值时,二面角
等于何值时,二面角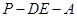 的大小为
的大小为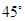 .
.
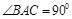 ,
,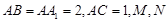 分别是
分别是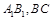 的中点。 (Ⅰ)证明:
的中点。 (Ⅰ)证明: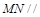 平面
平面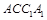 ;
;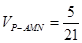 ,求
,求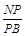 的值
的值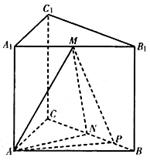
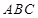 的边长为4,
的边长为4,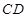 是
是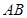 边上的高,
边上的高,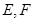 分别是
分别是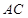
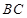 边的中点,现将△
边的中点,现将△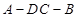 .
.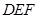 的位置关系,并说明理由;
的位置关系,并说明理由;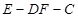 的余弦值;
的余弦值;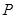 ,使
,使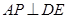 ?证明你的结论.
?证明你的结论.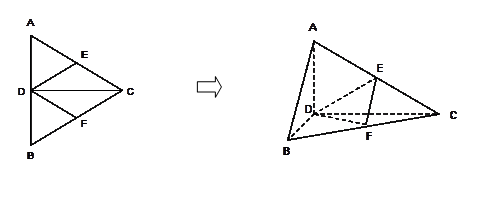
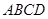 是直角梯形,
是直角梯形,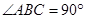 ,
,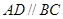 ,
,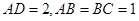 ,
,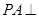 平面
平面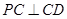 ;
;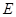 是
是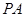 的中点,证明:
的中点,证明: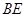 ∥平面
∥平面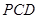 ;
;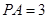 ,求三棱锥
,求三棱锥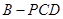 的体积.
的体积.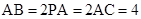 ,N为AB上一点且满足
,N为AB上一点且满足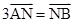 ,M,S分别为PB,BC的中点
,M,S分别为PB,BC的中点