题目内容
选修4-1:几何证明选讲
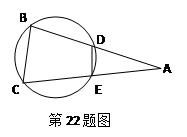
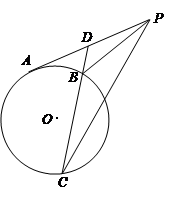
如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧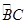 的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
(1)求证: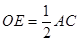 ;
;
(2)求证: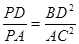
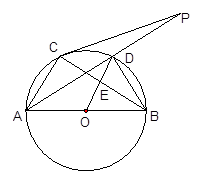
如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧
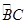 的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。(1)求证:
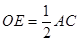 ;
; (2)求证:
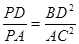
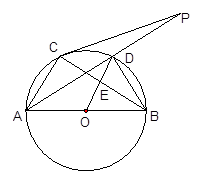
本试题主要是考查了平面几何中的证明。
证明: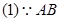 是⊙O的直径
是⊙O的直径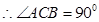 ,即
,即 ∵点D是劣弧
∵点D是劣弧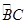 中点,由垂径定理得OD⊥BC∴OD//AC,又点O为AB中点∴
中点,由垂径定理得OD⊥BC∴OD//AC,又点O为AB中点∴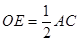
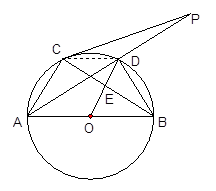
(2)连结CD
∵PC是⊙O的切线,∴∠PCD=∠PAC,又∠P为公共角,故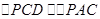
 ∵点D是劣弧
∵点D是劣弧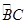 的中点∴CD=BD∴
的中点∴CD=BD∴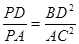
证明:
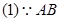 是⊙O的直径
是⊙O的直径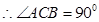 ,即
,即 ∵点D是劣弧
∵点D是劣弧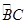 中点,由垂径定理得OD⊥BC∴OD//AC,又点O为AB中点∴
中点,由垂径定理得OD⊥BC∴OD//AC,又点O为AB中点∴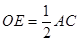
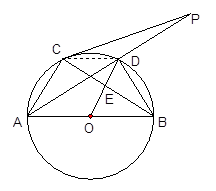
(2)连结CD
∵PC是⊙O的切线,∴∠PCD=∠PAC,又∠P为公共角,故
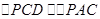
 ∵点D是劣弧
∵点D是劣弧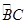 的中点∴CD=BD∴
的中点∴CD=BD∴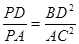

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
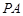 与⊙
与⊙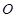 相切于点
相切于点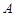 ,
,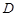 为
为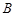 ,
,
 两点,若
两点,若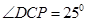 ,则
,则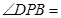 .
.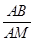 的值.
的值.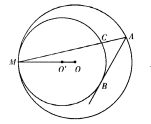
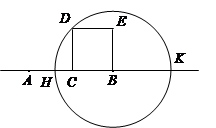
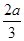 ,∠OAP=30°,则CP=_____
,∠OAP=30°,则CP=_____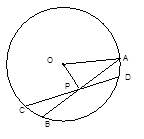
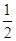 )=0
)=0