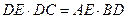题目内容
如图,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P, PD=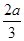 ,∠OAP=30°,则CP=_____
,∠OAP=30°,则CP=_____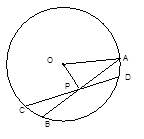
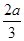 ,∠OAP=30°,则CP=_____
,∠OAP=30°,则CP=_____
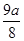
分析:利用垂径定理及其相交弦定理即可得出。
解答:
∵OP⊥AB,∴AP=PB.
在Rt△OAP中,
∵∠OAP=30°,OA=a,
∴AP=acos30°=
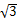 /2a,
/2a,由相交弦定理可得:
CP?PD=AP?PB,
∴CP=(
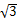 /2a)2/(2a/3)=9a/8
/2a)2/(2a/3)=9a/8点评:熟练掌握圆的垂径定理及其相交弦定理是解题的关键。

练习册系列答案
相关题目
 ,BE2=DE-EC.
,BE2=DE-EC. ;
;
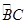 的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。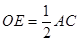 ;
; 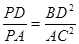
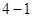 :几何证明选讲
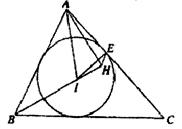
:几何证明选讲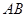 是圆
是圆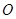 的直径,
的直径,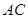 是弦,
是弦,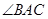 的平分线
的平分线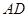 交圆
交圆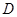 ,
,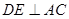 ,交
,交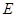 ,
,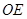 交
交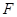 ,
,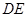 是圆
是圆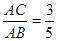 ,求
,求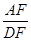 的值。
的值。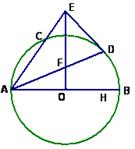
 ),动点B在直线
),动点B在直线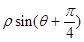 =
=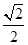 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 .
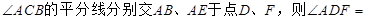 .
.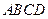 中,
中,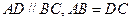 ,过点
,过点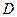 作
作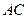 的平行线
的平行线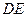 ,交
,交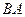 的延长线于点
的延长线于点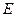 .求证:⑴
.求证:⑴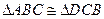 ⑵
⑵