题目内容
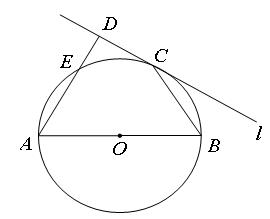
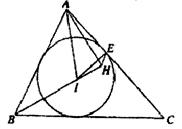
如图,设C为线段AB的中点,BCDE是以BC为一边的正方形,以B为圆心,BD为半径的圆与AB及其延长线相交于点H及K.
(Ⅰ)求证:HC·CK=BC2;
(Ⅱ)若圆的半径等于2,求AH·AK的值.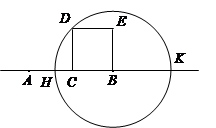
(Ⅰ)求证:HC·CK=BC2;
(Ⅱ)若圆的半径等于2,求AH·AK的值.
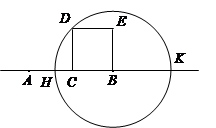
(Ⅰ)连结DH,DK,则DH⊥DK,
∴△DHC∽△KDC,∴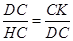 ,DC2=HC·CK,
,DC2=HC·CK,
又DC=BC,∴BC2=HC·CK………………(5分)
(Ⅱ)连结AD,则AD⊥BD,AD=BD,∴AD是⊙B的切线,于是AD2=AH·AK,
∴AH·AK=4
∴△DHC∽△KDC,∴
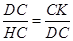 ,DC2=HC·CK,
,DC2=HC·CK,又DC=BC,∴BC2=HC·CK………………(5分)
(Ⅱ)连结AD,则AD⊥BD,AD=BD,∴AD是⊙B的切线,于是AD2=AH·AK,
∴AH·AK=4
(I)证明可以从结论出发进行寻找解题途径
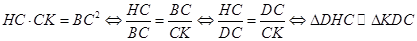 .
.
(II)证明AD为圆的切线之后,利用切割线定理即可求解
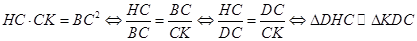 .
.(II)证明AD为圆的切线之后,利用切割线定理即可求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
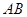 经过⊙
经过⊙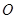 上的点
上的点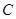 ,并且
,并且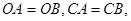 ⊙
⊙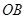 于
于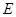 ,
,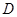 ,连接
,连接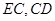 .
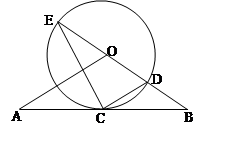
.
 ⊙
⊙ ,求
,求 的长.
的长.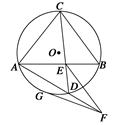
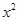 -7
-7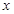 +12=0的两根,则
+12=0的两根,则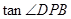 =_________。
=_________。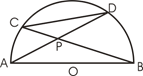
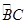 的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。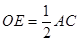 ;
; 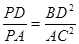
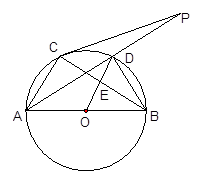
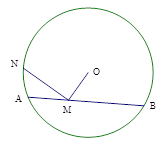
 为
为 的弦
的弦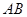 上的一点,连接
上的一点,连接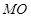 .
.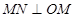 ,
,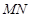 交圆于
交圆于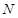 ,若
,若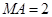 ,
,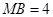 ,则
,则 .
.
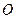 的直径
的直径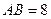 ,
,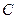 为圆周上一点,
为圆周上一点,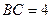 ,过
,过 ,过
,过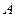 作直线
作直线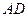 ,
,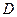 为垂足,
为垂足,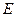 ,则线段
,则线段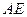 的长为 .
的长为 .