题目内容
18.(本小题满分14分)

如图5,四边形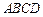 是圆柱
是圆柱 的轴截面,点
的轴截面,点 在圆柱
在圆柱 的底面圆周上,
的底面圆周上,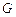 是
是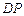 的中点,圆柱
的中点,圆柱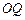 的底面圆的半径
的底面圆的半径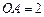 ,侧面积为
,侧面积为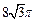 ,
,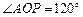 .
.
(1)求证: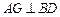 ;
;
(2)求二面角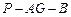 的平面角的余弦值.
的平面角的余弦值.

如图5,四边形
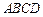 是圆柱
是圆柱 的轴截面,点
的轴截面,点 在圆柱
在圆柱 的底面圆周上,
的底面圆周上,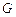 是
是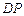 的中点,圆柱
的中点,圆柱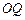 的底面圆的半径
的底面圆的半径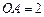 ,侧面积为
,侧面积为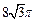 ,
,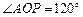 .
.(1)求证:
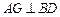 ;
;(2)求二面角
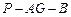 的平面角的余弦值.
的平面角的余弦值.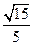
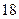 . (本小题满分
. (本小题满分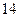 分)
分)(本题考查空间的线面关系、二面角、空间向量及坐标运算、圆柱的侧面积、余弦定理等知识,考查数形结合、化归转化的数学思想和方法,以及空间想象能力、推理论证能力和运算求解能力)
解:(1)(解法一):由题意可知
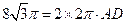 ,
,解得
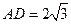 , …………
, ………… 分
分在
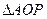 中,
中,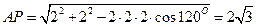 , …………
, …………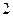 分
分∴
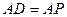 ,
,又 ∵
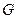 是
是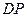 的中点,
的中点, ∴
∴ 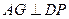 . ① …………
. ① …………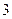 分
分∵
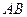 为圆
为圆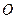 的直径,
的直径,∴
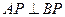 .
.由已知知
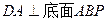 ,
,∴
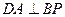 ,
,∴
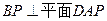 . …………
. …………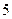 分
分∴
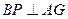 . ②
. ②∴ 由①②可知:
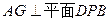 ,
,∴
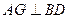 . …………
. …………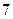 分
分(2)由(1)知:
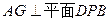 ,
,∴
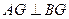 ,
,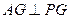 ,
,∴
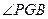 是二面角
是二面角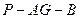 的平面角 . …………
的平面角 . ………… 分
分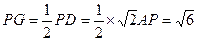 ,
, 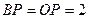 ,
, 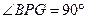 .
.∴
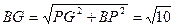 .
.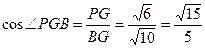 . ………
. ……… 分
分(解法二):建立如图所示的直角坐标系,
由题意可知
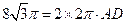 .
.解得
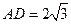 .
. 则
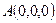 ,
,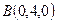 ,
,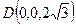 ,
,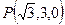 ,
,∵
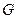 是
是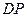 的中点,
的中点,∴ 可求得
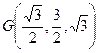 . …………
. …………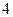 分
分(1)
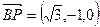 ,
,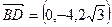 ,
,∴
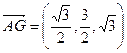 .
. ∵
∵ 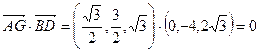 ,
,∴
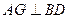 . …………
. ………… 分
分(2)由(1)知,
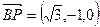 ,
, 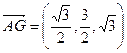 ,
,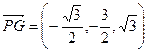 ,
, 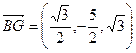 .
. ∵
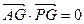 ,
,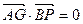 .
.∴
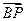 是平面
是平面 的法向量. …………
的法向量. ………… 分
分设
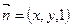 是平面
是平面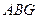 的法向量,
的法向量,由
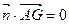 ,
,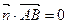 ,
,解得
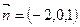 …………
…………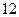 分
分 .
.所以二面角
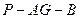 的平面角的余弦值
的平面角的余弦值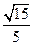 . …………
. …………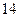 分
分
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
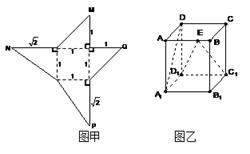
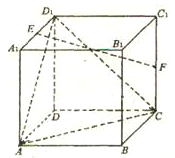
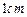 的正方体。
的正方体。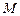 、
、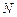 、
、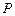 、
、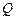 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积; 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;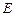 为棱
为棱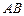 上的动点,试判断
上的动点,试判断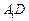 与平面
与平面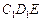 是否垂直,并说明理由。
是否垂直,并说明理由。
 中,
中,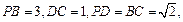
 为
为 边上一点,
边上一点,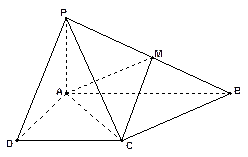
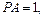 将
将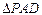 沿
沿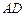 折起,使平面
折起,使平面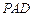 ⊥平面
⊥平面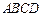 .
.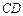 ⊥平面
⊥平面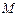 是侧棱
是侧棱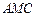 把几何体分成的两部分的体积之比。
把几何体分成的两部分的体积之比。 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.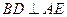
 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
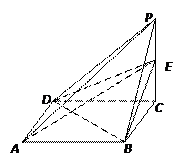
 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中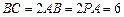 ,
,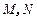 为侧棱
为侧棱 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.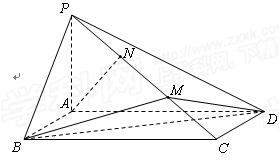
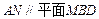 ;
;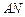 与
与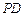 所成角的余弦值;
所成角的余弦值;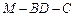 的余弦值.
的余弦值.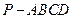 中,底面ABCD是菱形,
中,底面ABCD是菱形,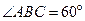 ,
,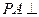 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且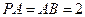
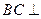 平面AMN;
平面AMN; 的体积;
的体积; 使得
使得 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。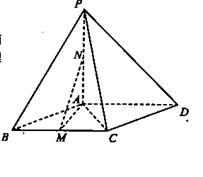
 的大小为
的大小为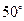 ,
,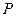 为空间中任意一点,则过点
为空间中任意一点,则过点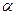 和平面
和平面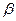 所成的角都是
所成的角都是 的直线的条数为( )
的直线的条数为( )
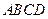 --
--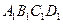 ,E、F分别是
,E、F分别是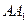 、
、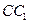 的中点,p是
的中点,p是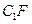 B、线段
B、线段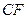 C、线段
C、线段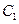 D、线段
D、线段