题目内容
(本小题满分14分)
如图:在四棱锥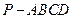 中,底面ABCD是菱形,
中,底面ABCD是菱形,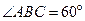 ,
,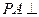 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且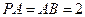
(I)证明: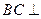 平面AMN;
平面AMN;
(II)求三棱锥N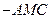 的体积;
的体积;
(III)在线段PD上是否存在一点E, 使得
使得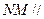 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。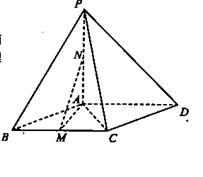
如图:在四棱锥
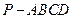 中,底面ABCD是菱形,
中,底面ABCD是菱形,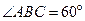 ,
,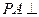 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且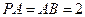
(I)证明:
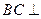 平面AMN;
平面AMN;(II)求三棱锥N
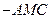 的体积;
的体积;(III)在线段PD上是否存在一点E,
 使得
使得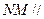 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。
证明:(I)因为ABCD为菱形,所以AB=BC
又∠ABC=60°,所以AB=BC=AC, ………………1分
又M为BC中点,所以BC⊥AM ………………2分
而PA⊥平面ABCD,BC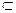 平面ABCD,所以PA⊥BC ………………4分
平面ABCD,所以PA⊥BC ………………4分
又PA∩AM=A,所以BC⊥平面AMN ………………5分
(II)因为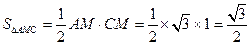 ………………6分
………………6分
又PA⊥底面ABCD,PA=2,所以AN=1
 所以,三棱锥N—AMC的体积
所以,三棱锥N—AMC的体积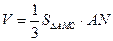 ………………8分
………………8分
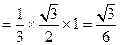 ………………9分
………………9分
(III)存在 ………………10分
取PD中点E,连结NE,EC,AE,
因为N,E分别为PA,PD中点,所以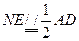 ………………11分
………………11分
又在菱形ABCD中,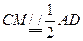
所以NE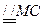 ,即MCEN是平行四边形 ………………12分
,即MCEN是平行四边形 ………………12分
所以,NM//EC,
又EC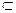 平面ACE,NM
平面ACE,NM 平面ACE
平面ACE
所以MN//平面ACE, ………………13分
即在PD上存在一点E,使得NM//平面ACE,
此时
又∠ABC=60°,所以AB=BC=AC, ………………1分
又M为BC中点,所以BC⊥AM ………………2分
而PA⊥平面ABCD,BC
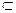 平面ABCD,所以PA⊥BC ………………4分
平面ABCD,所以PA⊥BC ………………4分又PA∩AM=A,所以BC⊥平面AMN ………………5分
(II)因为
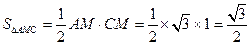 ………………6分
………………6分又PA⊥底面ABCD,PA=2,所以AN=1
 所以,三棱锥N—AMC的体积
所以,三棱锥N—AMC的体积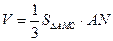 ………………8分
………………8分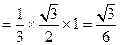 ………………9分
………………9分(III)存在 ………………10分
取PD中点E,连结NE,EC,AE,
因为N,E分别为PA,PD中点,所以
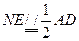 ………………11分
………………11分又在菱形ABCD中,
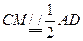
所以NE
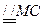 ,即MCEN是平行四边形 ………………12分
,即MCEN是平行四边形 ………………12分所以,NM//EC,
又EC
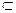 平面ACE,NM
平面ACE,NM 平面ACE
平面ACE所以MN//平面ACE, ………………13分
即在PD上存在一点E,使得NM//平面ACE,
此时

略

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
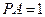 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。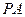 ⊥
⊥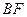 ;
;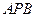 与面
与面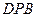 所成二面角的大小。
所成二面角的大小。
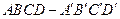 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥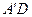 ,截面PQGH∥
,截面PQGH∥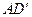 .
.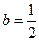 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.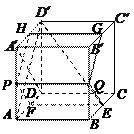

 是圆柱
是圆柱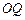 的轴截面,点
的轴截面,点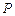 在圆柱
在圆柱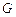 是
是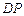 的中点,圆柱
的中点,圆柱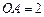 ,侧面积为
,侧面积为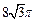 ,
,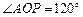 .
.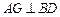 ;
;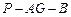 的平面角的余弦值.
的平面角的余弦值. 倍
倍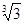 倍
倍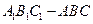 中,
中,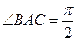 ,
,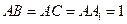 . 已知G与E分别为
. 已知G与E分别为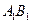 和
和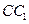 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和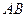 上的动点(不包括端点). 若
上的动点(不包括端点). 若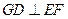 ,则线段
,则线段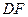 的长度的取值范围为
的长度的取值范围为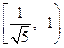



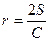 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。