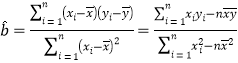题目内容
【题目】已知定义在R上的偶函数f(x),满足f(x+4)=-f(x)+f(2),且在区间[0,4]上是增函数,下列命题中正确的是( )
A.函数f(x)的一个周期为4
B.直线x=-4是函数f(x)图象的一条对称轴
C.函数f(x)在[-6,-5)上单调递增,在[-5,-4)上单调递减
D.函数f(x)在[0,100]内有25个零点
【答案】ABD
【解析】
根据函数的奇偶性和条件,得到![]() ,即函数是周期为4的周期函数,结合的周期性,奇偶性以及对称性的性质分别进行判断即可.
,即函数是周期为4的周期函数,结合的周期性,奇偶性以及对称性的性质分别进行判断即可.
![]() 偶函数
偶函数![]() ,满足
,满足![]() ,
,![]() 令
令![]() 得
得![]() ,
,
即![]() ,得
,得![]() ,
,
则![]() ,
,
即函数![]() 是周期为4的周期函数,
是周期为4的周期函数,
故A正确;![]() 是偶函数,
是偶函数,![]() 图象关于y轴即
图象关于y轴即![]() 对称,函数的周期是4,
对称,函数的周期是4,![]() 是函数
是函数![]() 图象的一条对称轴,
图象的一条对称轴,
故B正确;![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() 在区间
在区间![]() 上是减函数,
上是减函数,
则在区间![]() 上是减函数,
上是减函数,
故C错误;![]() ,
,![]() 在区间
在区间![]() 上是减函数,
上是减函数,![]() 在区间
在区间![]() 上是减函数,
上是减函数,
即函数在一个周期![]() 内只有一个零点,
内只有一个零点,
则函数![]() 在
在![]() 内有25个零点,故D正确.
内有25个零点,故D正确.
故选:ABD.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量![]() =(sinA+sinC,sinB),
=(sinA+sinC,sinB),![]() =(c﹣b,c﹣a),且
=(c﹣b,c﹣a),且![]() ∥
∥![]() .
.
(1)求角A的大小;
(2)若a=3,b+c=5,求△ABC的面积.
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 |
|
|
|
|
|
管理时间 |
|
|
|
|
|
并调查了某村![]() 名村民参与管理的意愿,得到的部分数据如下表所示:
名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 |
|
|
女性村民 |
|
![]() 求出相关系数
求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
![]() 若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取
若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取![]() 人,记取到不愿意参与管理的男性村民的人数为
人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]()