题目内容
【题目】已知函数![]() 函数
函数![]() 与直线
与直线![]() 相切,设函数
相切,设函数![]() 其中a、c∈R,e是自然对数的底数.
其中a、c∈R,e是自然对数的底数.
(1)讨论h(x)的单调性;
(2)h(x)在区间![]() 内有两个极值点.
内有两个极值点.
①求a的取值范围;
②设函数h(x)的极大值和极小值的差为M,求实数M的取值范围.
【答案】(1)答案见解析(2)①![]() ②
②![]()
【解析】
![]() 直接利用导数的几何意义即可求得c值,得
直接利用导数的几何意义即可求得c值,得![]() ,求导,分类讨论即可求解;
,求导,分类讨论即可求解;![]() ①函数
①函数![]() 在区间
在区间![]() 内有两个极值点,
内有两个极值点,![]() ,则
,则![]() 在区间
在区间![]() 内有两个不同的根即可;②
内有两个不同的根即可;②![]() 的极大值和极小值的差为
的极大值和极小值的差为![]() 进行化简分析.
进行化简分析.
![]() 设直线
设直线![]() 与函数
与函数![]() 相切与点
相切与点![]() ,
,
函数![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ,
,![]() ,
,
把![]() ,
,![]() 代入上式得
代入上式得![]() ,
,![]() .
.
所以,实数c的值为2.
所以![]() ,
,![]()
则![]() ,
,
当![]() 时,
时, ![]() ,
,
故函数![]() 在
在![]() 上单调递减,无增区间,
上单调递减,无增区间,
当![]() 时,
时,![]() ,
,
![]() ,
,
所以函数![]() 在
在![]() 上单调递增,无减区间,
上单调递增,无减区间,
当![]() 时,令
时,令![]() ,
,
解得![]() ,
,
所以当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
![]() 由
由![]() 知
知![]() ,
,
设函数![]() 在区间
在区间![]() 内有两个极值点
内有两个极值点![]() ,
,![]() ,
,
令![]() ,
,
则![]() ,设
,设![]()
因为![]() ,故只需
,故只需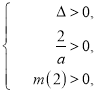
所以,![]() .
.
![]() 因为
因为![]() ,
,
所以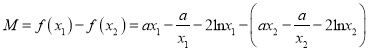

![]() .
.
由![]() ,得
,得![]() ,且
,且![]() .
.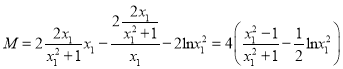 .
.
设![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() ,
,
所以,实数M的取值范围是![]() .
.

【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数)
(1)A类工人中和B类工人各抽查多少工人?
(2)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2:
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 | x | 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 | y | 36 | 18 |
①先确定x,y,再在答题纸上完成下列频率分布直方图.就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)

图1A类工人生产能力的频率分布直方图 图2B类工人生产能力的频率分布直方图