题目内容
【题目】若动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离之和为
的距离之和为![]() .
.
(1)求点![]() 的轨迹方程,并在答题卡所示位置画出方程的曲线草图;
的轨迹方程,并在答题卡所示位置画出方程的曲线草图;
(2)(理)记(1)得到的轨迹为曲线![]() ,问曲线
,问曲线![]() 上关于点
上关于点![]() 对称的不同点有几对?请说明理由.
对称的不同点有几对?请说明理由.
(3)(文)记(1)得到的轨迹为曲线![]() ,若曲线
,若曲线![]() 上恰有三对不同的点关于点
上恰有三对不同的点关于点![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
【答案】(1)点![]() 的轨迹方程为
的轨迹方程为![]() ,作图见解析 (2)答案不唯一 ,见解析(3)
,作图见解析 (2)答案不唯一 ,见解析(3)![]()
【解析】
(1)根据条件列方程,化简即得轨迹方程,再根据轨迹形状画图;
(2)结合图象易得关于![]() 轴对称点的个数,再利用方程求解不关于
轴对称点的个数,再利用方程求解不关于![]() 轴对称点的个数,最后综合得结果;
轴对称点的个数,最后综合得结果;
(3)结合图象易得关于![]() 轴对称点的有一对,再利用方程求解不关于
轴对称点的有一对,再利用方程求解不关于![]() 轴对称点的对数为两对的条件,即得结果.
轴对称点的对数为两对的条件,即得结果.
解:![]() 、设
、设![]() ,由题意
,由题意![]()
①:当![]() 时,有
时,有![]() ,化简得:
,化简得:![]()
②:当![]() 时,有
时,有![]() ,化简得:
,化简得:![]() (二次函数)
(二次函数)
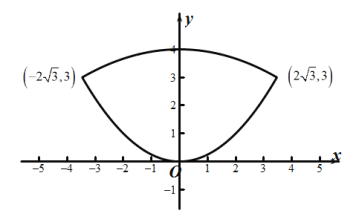
综上所述:点![]() 的轨迹方程为
的轨迹方程为![]() (如图)
(如图)
![]() 、(理)当
、(理)当![]() 或
或![]() 显然不存在符合题意的对称点
显然不存在符合题意的对称点
当![]() 时,注意到曲线
时,注意到曲线![]() 关于
关于![]() 轴对称,至少存在一对(关于
轴对称,至少存在一对(关于![]() 轴对称的)对称点
轴对称的)对称点
下面研究曲线![]() 上关于
上关于![]() 对称但不关于
对称但不关于![]() 轴对称的对称点
轴对称的对称点
设![]() 是轨迹
是轨迹![]()
![]() 上任意一点,则
上任意一点,则![]() ,它关于
,它关于![]() 的对称点为
的对称点为![]() ,由于点
,由于点![]() 在轨迹
在轨迹![]() 上,
上,

所以![]() ,
,
联立方程组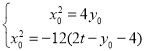 (*)得
(*)得![]() ,
,
化简得![]()
①当![]() 时,
时,![]() ,此时方程组(*)有两解,即增加有两组对称点。
,此时方程组(*)有两解,即增加有两组对称点。
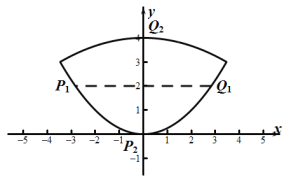
②当![]() 时,
时,![]() ,此时方程组(*)只有一组解,即增加一组对称点。(注:对称点为
,此时方程组(*)只有一组解,即增加一组对称点。(注:对称点为![]() ,
,![]() )
)
③当![]() 时,
时,![]() ,此时方程组(*)有两解为
,此时方程组(*)有两解为![]() ,没有增加新的对称点。
,没有增加新的对称点。

综上所述:
(3)、(文)若![]() ,则
,则![]() ,所以曲线
,所以曲线![]() 关于
关于![]() 轴对称,
轴对称,
所以一对存在关于![]() 轴对称的对称点
轴对称的对称点
下面研究曲线![]() 上关于
上关于![]() 对称但不关于
对称但不关于![]() 轴对称的对称点
轴对称的对称点
设![]() 是轨迹
是轨迹![]()
![]() 上任意一点,则
上任意一点,则![]() ,它关于
,它关于![]() 的对称点为
的对称点为![]() ,由于点
,由于点![]() 在轨迹
在轨迹![]() 上,
上,

所以![]() ,联立方程组
,联立方程组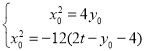 (*)得
(*)得![]() ,化简得
,化简得![]()
当![]() 时,
时,![]() ,此时方程组(*)有两解,即增加有两组对称点。
,此时方程组(*)有两解,即增加有两组对称点。
所以![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目