题目内容
17.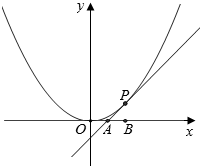 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).(Ⅰ)若动点Q满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$+$\sqrt{2}$|$\overrightarrow{AQ}$|=0,求点Q的轨迹C的方程;
(Ⅱ)设椭圆Γ的中心在原点,对称轴在坐标轴上,直线l:y=kx+t(k≠0,t≠0)与轨迹C交于M,N两点,且与椭圆Γ交于H,K两点.若线段MN与线段HK的中点重合,求椭圆Γ的离心率.
分析 (I)对抛物线方程进行求导,求得直线l的斜率,设出Q的坐标,利用$\overrightarrow{AB}$•$\overrightarrow{BQ}$+$\sqrt{2}$|$\overrightarrow{AQ}$|=0求得x和y的关系.
(II)设椭圆E的方程,根据M,N在椭圆C上,设点的坐标,代入两式相减并恒等变形得斜率,同理由H,K在椭圆E上,得斜率,利用弦AB的中点与弦HK的中点重合,建立方程,从而可得椭圆E的离心率,即可得到结论.
解答 解:(Ⅰ)由x2=4y得y=$\frac{1}{4}{x}^{2}$,∴y′=$\frac{1}{2}$x.
∴直线l的斜率为y′|x=2=1,
故l的方程为y=x-1,∴点A的坐标为(1,0).
设Q(x,y),则$\overrightarrow{AB}$=(1,0),$\overrightarrow{BQ}$=(x-2,y),$\overrightarrow{AQ}$=(x-1,y),
由$\overrightarrow{AB}$•$\overrightarrow{BQ}$+$\sqrt{2}$|$\overrightarrow{AQ}$|=0,
整理,得$\frac{{x}^{2}}{2}+{y}^{2}=1$..
(II)设椭圆Γ的方程为$\frac{{x}^{2}}{{m}^{2}}+\frac{{y}^{2}}{{n}^{2}}=1$(m>0,n>0,m≠n),并设M(x1,y1),N(x2,y2),H(x3,y3),K(x4,y4).
∵M,N在椭圆C上,
∴x12+2y12=2,且x22+2y22=2,两式相减并恒等变形得k=-2×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$.
由H,K在椭圆E上,仿前述方法可得k=-$\frac{{m}^{2}{x}_{3}+{x}_{4}}{{n}^{2}{y}_{3}+{y}_{4}}$.
∵弦AB的中点与弦HK的中点重合,∴m2=2n2,
求得椭圆E的离心率e=$\frac{\sqrt{{m}^{2}-{n}^{2}}}{m}$=$\frac{\sqrt{2}}{2}$.
点评 本题主要考查椭圆的标准方程、圆锥曲线的性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查分类整合思想、数形结合思想、化归转化思想等.

 学习实践园地系列答案
学习实践园地系列答案| A. | $\frac{BC}{sinα}=\frac{AD}{sinβ}$ | B. | $\frac{AD}{sinα}=\frac{BC}{sinβ}$ | ||
| C. | $\frac{{{S_{△BCD}}}}{sinα}=\frac{{{S_{△ACD}}}}{sinβ}$ | D. | $\frac{{{S_{△ACD}}}}{sinα}=\frac{{{S_{△BCD}}}}{sinβ}$ |
 已知椭圆C中心在坐标原点,对称轴为坐标轴,且过点A(2$\sqrt{6}$,2)、B(3,3).
已知椭圆C中心在坐标原点,对称轴为坐标轴,且过点A(2$\sqrt{6}$,2)、B(3,3).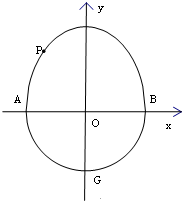 半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0,如图所示,曲线C交x轴于A,B两点,交y轴负半轴于点G.椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是它的一个焦点,点P是曲线C位于x轴上方的任意一点,且△PFG的周长是$2\sqrt{2}+2$.
半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0,如图所示,曲线C交x轴于A,B两点,交y轴负半轴于点G.椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是它的一个焦点,点P是曲线C位于x轴上方的任意一点,且△PFG的周长是$2\sqrt{2}+2$. 如图,三棱锥C-ABD中,C是以AB为直径的半圆上一点,点E在直径AB上,已知AB=10,AC=2$\sqrt{5}$,CE=4,CD=3$\sqrt{2}$,AD=DE=$\sqrt{2}$.
如图,三棱锥C-ABD中,C是以AB为直径的半圆上一点,点E在直径AB上,已知AB=10,AC=2$\sqrt{5}$,CE=4,CD=3$\sqrt{2}$,AD=DE=$\sqrt{2}$.