题目内容

18．设n∈N*，（x+3）n展开式的所有项系数和为256，则其二项式系数的最大值为6．（用数字作答）

分析 由题意求得n，再由二项式系数的性质求得其二项式系数的最大值．

解答 解：由（x+3）n展开式的所有项系数和为256，得4n=256，即n=4．
∴（x+3）n =（x+3）4，其展开式中有5项，其中二项式系数最大的是第3项，
二项式系数的最大值为${C}_{4}^{2}=6$．
故答案为：6．

点评 本题考查二项式系数的性质，考查了二项展开式的二项式系数和项的系数，是基础题．

练习册系列答案
相关题目
8．若角β的终边上一点A（-5，m），且tanβ=5，则m=-25，并求β的其它三角函数值．
9．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与抛物线y2=4x的焦点重合，则a+b的最大值为（　　）
A．$\sqrt{2}$B．1C．$\frac{\sqrt{2}}{2}$D．2$\sqrt{2}$
6．已知向量$\overrightarrow{m}$=（sinA，sinB），$\overrightarrow{n}$=（cosB，cosA），$\overrightarrow{m}$•$\overrightarrow{n}$=sin2C，且A，B，C分别为△ABC的三边a，b，c所对的角．
（I）求角C的大小；
（Ⅱ）若sinA，sinC，sinB成等差数列，且△ABC的面积为$9\sqrt{3}$，求c边的长．
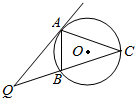13．如图，直线PQ与⊙O相切于点A，AB是⊙O的弦，∠PAB的平分线AC交⊙O于点C，连结CB，并延长与直线PQ相交于点Q，若AQ=6，AC=5．
（Ⅰ）求证：QC2-QA2=BC•QC；
（Ⅱ）求弦AB的长．
3．某业余俱乐部由10名乒乓球队员和5名羽毛球队员组成，其中乒乓球队员中有4名女队员；羽毛球队员中有2名女队员，现采用分层抽样方法（按乒乓球队和羽毛球队分层，在每一层内采用简单随机抽样）从这15人中共抽取3名队员参加一项比赛．
（Ⅰ）求所抽取的3名队员中乒乓球队员、羽毛球队员的人数；
（Ⅱ）求从乒乓球队抽取的队员中至少有1名女队员的概率；
（Ⅲ）记ξ为抽取的3名队员中男队员人数，求ξ的分布列及数学期望．
10．设i为虚数单位，复数$\frac{1-i}{i}$=-1-i．
7．已知函数f（x）=ax2+2bx，g（x）=b+lnx（a∈[-1，2]，b∈R，b≠0）．
（Ⅰ）求命题A：“?x∈R，对于?m∈R+，f（x）=m”为真命题的概率；
（Ⅱ）若a∈Z，b∈{-2，-1，1，2}，写出所有的数对（a，b）．设函数φ（x）=$\left\{\begin{array}{l}f（x），x≤1\\ g（x），x＞1\end{array}$记“?x1，x2∈（-∞，+∞），x1≠x2，$\frac{{φ（{x_1}）-φ（{x_2}）}}{{{x_1}-{x_2}}}$＞0”为事件B，求事件B发生的概率P（B）．
8．已知数列{an}与{bn}满足：a1+a2+a3+…+an=log2bn（n∈N*）．若{an}为等差数列，且a1=2，b3=64b2．
（Ⅰ）求an与bn；
（Ⅱ）设cn═（an+n+1）•2${\;}^{{a}_{n}-2}$，求数列{cn}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网