题目内容
6.已知向量$\overrightarrow{m}$=(sinA,sinB),$\overrightarrow{n}$=(cosB,cosA),$\overrightarrow{m}$•$\overrightarrow{n}$=sin2C,且A,B,C分别为△ABC的三边a,b,c所对的角.(I)求角C的大小;
(Ⅱ)若sinA,sinC,sinB成等差数列,且△ABC的面积为$9\sqrt{3}$,求c边的长.
分析 (Ⅰ)根据向量数量积的定义,以及三角函数的关系式即可求角C的大小;
(Ⅱ)若根据等差数列的性质,建立方程关系结合三角形的面积公式以及余弦定理进行求解即可.
解答 解:(Ⅰ)$\overrightarrow{m}$•$\overrightarrow{n}$=sinAcosB+sinBcosA=sin(A+B)=sin(π-C)=sinC,
∵$\overrightarrow{m}$•$\overrightarrow{n}$=sin2C,
∴$\overrightarrow{m}$•$\overrightarrow{n}$=sin2C=sinC,
即2sinCcosC=sinC,解得cosC=$\frac{1}{2}$,
C=$\frac{π}{3}$.
(Ⅱ)∵sinA,sinC,sinB成等差数列,
∴2sinC=sinA+sinB,
由正弦定理得2c=a+b,
又△ABC的面积为$9\sqrt{3}$,
即$\frac{1}{2}$absinC=$9\sqrt{3}$,
即$\frac{1}{2}×\frac{\sqrt{3}}{2}$ab=$9\sqrt{3}$,解得ab=36,
由余弦定理c2=a2+b2-2abcosC=(a+b)2-3ab,
得c2=4c2-3×36,
解得c2=36,c=6.
点评 本题主要考查余弦定理和三角形的面积的计算,利用向量的数量积进行化简是解决本题的关键.考查学生的运算能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
14.已知函数f(x)=ex的图象与函数g(x)=|ln(-x)|的图象有两个交点A(x1,y1),B(x2,y2),则( )
| A. | $\frac{1}{10}$<x1x2<$\frac{1}{e}$ | B. | $\frac{1}{e}$<x1x2<1 | C. | 1<x1x2<e | D. | x1x2>e |
11.若定义在R上的函数满足f(-x)=f(x),f(4-x)=f(x),且当x∈[0,2]时,f(x)=$\sqrt{4-{x^2}}$,则函数H(x)=|xex|-f(x)在区间[-6,2]上的零点个数为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
15.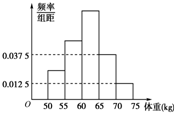 为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a,b,c恰成等差数列,若抽取的学生人数是48,则第2小组的频数为( )
为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a,b,c恰成等差数列,若抽取的学生人数是48,则第2小组的频数为( )
 为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a,b,c恰成等差数列,若抽取的学生人数是48,则第2小组的频数为( )
为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a,b,c恰成等差数列,若抽取的学生人数是48,则第2小组的频数为( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
16.二次函数y=kx2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n为正整数,a1=$\frac{1}{3}$,若数列{an}的前n项和为Sn,则S5=( )
| A. | $\frac{3}{2}[{1-{{({\frac{1}{3}})}^5}}]$ | B. | $\frac{1}{3}[{1-{{({\frac{1}{3}})}^5}}]$ | C. | $\frac{2}{3}[{1-{{({\frac{1}{2}})}^5}}]$ | D. | $\frac{3}{2}[{1-{{({\frac{1}{2}})}^5}}]$ |