��Ŀ����
7����֪����f��x��=ax2+2bx��g��x��=b+lnx��a��[-1��2]��b��R��b��0��������������A����?x��R������?m��R+��f��x��=m��Ϊ������ĸ��ʣ�
������a��Z��b��{-2��-1��1��2}��д�����е����ԣ�a��b�����躯���գ�x��=$\left\{\begin{array}{l}f��x����x��1\\ g��x����x��1\end{array}$�ǡ�?x1��x2�ʣ�-�ޣ�+�ޣ���x1��x2��$\frac{{�գ�{x_1}��-�գ�{x_2}��}}{{{x_1}-{x_2}}}$��0��Ϊ�¼�B�����¼�B�����ĸ���P��B����
���� ����a��0ʱ������AΪ�����⣬������AΪ�����⣬����a��0�����ü��θ�����ø��ʣ�
�����ȵó����п��ܵ����ԣ��ٸ��ݺ����õ����Եõ�����Ҫʹ�¼�B������ֻ��f��1����g��1���̶��ó����ۣ�
��� �⣺����a��0ʱ������AΪ�����⣬������AΪ�����⣬����a��0��
��-1��a��3���ɼ��θ���֪ʶ�ɵ�����AΪ������ĸ���ΪP��A��=$\frac{2}{3}$
�������п��ܵ����ԣ�a��b��Ϊ��-1��-2����-1��-1������-1��1������-1��2������0��-2����0��-1����
��0��1������0��2������1��-2������1��-1������1��1������1��2������2��-2������2��-1������2��1������2��2��������16����
��Ϊx��1ʱ���գ�x��=g��x��=b+lnx�����䣨1��+�ޣ�������������
����?x1��x2��[1��+�ޣ���x1��x2��$\frac{�գ�{x}_{1}��-�գ�{x}_{2}��}{{x}_{1}-{x}_{2}}��0$����������Ҫʹ�¼�B������ֻ��f��1����g��1��
��a+b��0���������������ԣ�a��b��Ϊ��-1��-2����-1��-1������-1��1����������0��-2����0��-1������1��-2������1��-1������2��-2������8����
�����ɹŵ����֪ʶ�ɵ�P��B��=$\frac{8}{16}=\frac{1}{2}$��
���� ������Ҫ����ŵ���ͺͼ��θ��ͣ��������ͣ��߿�ʱ�п��飮

| A�� | $\frac{3}{2}[{1-{{��{\frac{1}{3}}��}^5}}]$ | B�� | $\frac{1}{3}[{1-{{��{\frac{1}{3}}��}^5}}]$ | C�� | $\frac{2}{3}[{1-{{��{\frac{1}{2}}��}^5}}]$ | D�� | $\frac{3}{2}[{1-{{��{\frac{1}{2}}��}^5}}]$ |
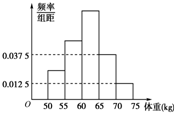 Ϊ���˽�ij�ؽ���߿�����������רҵ��ѧ������������������õ�ѧ���������ݷ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3С���Ƶ��a��b��cǡ�ɵȲ����У�����ȡ��ѧ��������48�����2С���Ƶ��Ϊ��������
Ϊ���˽�ij�ؽ���߿�����������רҵ��ѧ������������������õ�ѧ���������ݷ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3С���Ƶ��a��b��cǡ�ɵȲ����У�����ȡ��ѧ��������48�����2С���Ƶ��Ϊ��������


