题目内容
13.在(x-1)4-(x-1)5+(x-1)6-(x-1)7的展开式中,含x3的项的系数是-69.(用数字作答)分析 利用二项展开式的通项公式,分别求出的四部分中含x3的项的系数得答案.
解答 解:(x-1)4-(x-1)5+(x-1)6-(x-1)7的展开式中,含x3的项的系数是:
${-C}_{4}^{1}-{C}_{5}^{2}-{C}_{6}^{3}-{C}_{7}^{3}$=-4-10-20-35=-69.
故答案为:-69.
点评 本题考查利用二项展开式的通项公式解决展开式的特定项问题,属于基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
3.已知tanα=-$\frac{3}{5}$,则cos2($\frac{π}{4}$+α)=( )
| A. | $\frac{16}{17}$ | B. | $\frac{15}{17}$ | C. | $\frac{9}{17}$ | D. | $\frac{8}{17}$ |
1.已知命题p:?α∈R,cos (π-α)=cos α;命题q:?x∈R,x2+1>0.则下面结论正确的是( )
| A. | p∨q是真命题 | B. | p∧q是假命题 | C. | ¬q是真命题 | D. | p 是假命题 |
3.某大学的一个社会实践调查小组,在对大学生的良好“光盘习惯”的调査中,随机发放了l20份问巻.对收回的l00份有效问卷进行统计,得到如下2x2列联表:
(1)现已按是否能做到光盘分层从45份女生问卷中抽取了9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为ξ,试求随机变量ξ的分布列和数学期望
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么根据临界值表最精确的P的值应为多少?请说明理由.
附:独立性检验统计量K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d,
独立性检验临界表:
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么根据临界值表最精确的P的值应为多少?请说明理由.
附:独立性检验统计量K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d,
独立性检验临界表:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
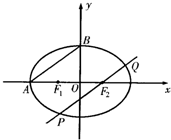 如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.
如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.