题目内容
5.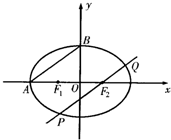 如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.
如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)作与AB平行的直线l交椭圆于P、Q两点,|PQ|=$\frac{9\sqrt{5}}{5}$,求直线l的方程.
分析 (Ⅰ)由题意可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{5}}{5}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{2}ab=\sqrt{5}}\end{array}\right.$,从而解得;
(Ⅱ)由题意设直线PQ的方程为y=$\frac{2\sqrt{5}}{5}$x+m,与椭圆C的方程$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1联立化简可得8x2+4$\sqrt{5}$bx+5m2-20=0,从而由韦达定理及距离公式可得$\frac{9}{5}$(10-$\frac{5}{4}$m2)=$\frac{81}{5}$,从而解出m即可.
解答 解:(Ⅰ)由题意得,
$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{5}}{5}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{2}ab=\sqrt{5}}\end{array}\right.$,
解得,a=$\sqrt{5}$,b=2,c=1;
故椭圆C的方程为$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)直线PQ的斜率k=$\frac{2\sqrt{5}}{5}$,
故设直线PQ的方程为y=$\frac{2\sqrt{5}}{5}$x+m,
与椭圆C的方程$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1联立化简可得,
8x2+4$\sqrt{5}$bx+5m2-20=0,
故x1+x2=-$\frac{\sqrt{5}}{2}$m,x1x2=$\frac{1}{8}$(5m2-20),
故(1+($\frac{2\sqrt{5}}{5}$)2)((-$\frac{\sqrt{5}}{2}$m)2-4×$\frac{1}{8}$(5m2-20))=($\frac{9\sqrt{5}}{5}$)2,
即$\frac{9}{5}$(10-$\frac{5}{4}$m2)=$\frac{81}{5}$,
即10-$\frac{5}{4}$m2=9,
故$\frac{5}{4}$m2=1,
故m=±$\frac{2\sqrt{5}}{5}$;
故直线l的方程为y=$\frac{2\sqrt{5}}{5}$x+±$\frac{2\sqrt{5}}{5}$;即2$\sqrt{5}$x-5y±2$\sqrt{5}$=0.
点评 本题考查了椭圆的标准方程的应用及韦达定理与两点间距离公式的应用,属于中档题.

| A. | ($\frac{1}{4}$,1+$\frac{\sqrt{2}}{2}$] | B. | ($\frac{1}{4}$,1] | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
 如图,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四条边上,若直线EF与GH相交,则它们的交点M必在直线AC上.
如图,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四条边上,若直线EF与GH相交,则它们的交点M必在直线AC上.