题目内容
【题目】设函数![]() ,且
,且![]() (其中e是自然对数的底数).
(其中e是自然对数的底数).
(Ⅰ)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)增区间为![]() ,减区间为
,减区间为![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)当![]() 时
时![]() ,令
,令![]() ,对
,对![]() 求导分析出其单调性,从而分析出函数值的符号,得到
求导分析出其单调性,从而分析出函数值的符号,得到![]() 的单调区间.
的单调区间.
(Ⅱ)对![]() 求导讨论其单调性,分析其最小值,证明其最小值大于0即可.
求导讨论其单调性,分析其最小值,证明其最小值大于0即可.
(Ⅰ)由![]() 可得,
可得,![]() ,又
,又![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调增函数,又
单调增函数,又![]() .
.
∴当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ;
;![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,减区间为
,减区间为![]()
(Ⅱ)当![]() 时,
时,![]() ,符合题意.
,符合题意.
方法(一)当![]() 时,
时,![]()
令![]() ,又
,又![]() ,
,![]()
∴![]() 在
在![]() 唯一的零点,设为
唯一的零点,设为![]() ,有
,有![]()
且![]() ,
,![]() ,
,![]() 单调递减;
单调递减;![]() ,
,![]() ,
,![]() 单调递增
单调递增
∴![]() ∵
∵![]() ,∴
,∴![]() ,两边取对数,
,两边取对数,
![]() ∴
∴![]()
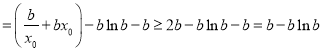 (当且仅当
(当且仅当![]() 时到等号)
时到等号)
设![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
又![]() ,且,
,且,![]() ,趋向0时,
,趋向0时,![]() ;
;
∴当![]() ,
,![]() ,当且仅当
,当且仅当![]() 时取等号
时取等号
由(1)可知,当![]() 时,
时,![]() ,故当
,故当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]()
综上,当![]() 时,
时,![]()
方法(二)
当![]() 时,(i)当
时,(i)当![]() 时
时
![]() ,
,![]() ,
,![]() 显然成立;
显然成立;
(ii)当![]() 时,构造函数
时,构造函数![]()
![]() ,
,![]() 在
在![]() 为减函数,∴
为减函数,∴![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
∴![]()
又由![]() ,可得
,可得![]() ,进而
,进而![]()
综上:当![]() 时,
时,![]()

【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)求![]() 与
与![]() 的相关系数
的相关系数![]() 精确到0.01,并判断
精确到0.01,并判断![]() 与
与![]() 的关系是否可用线性回归方程模型拟合?(规定:
的关系是否可用线性回归方程模型拟合?(规定:![]() 时,可用线性回归方程模型拟合);
时,可用线性回归方程模型拟合);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型
,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:(1)相关系数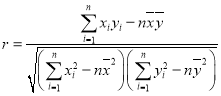
(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
