题目内容
【题目】记点
到图形
上每一个点的距离的最小值称为点到图形的距离，那么平面内到定圆的距离与到定点
的距离相等的点的轨迹不可能是 （ ）
A.圆B.椭圆C.双曲线的一支D.直线
【答案】D
【解析】
根据题意“点P到图形C上每一个点的距离的最小值称为点P到图形C的距离”，将平面内到定圆C的距离转化为到圆上动点的距离，再分点A现圆C的位置关系，结合圆锥曲线的定义即可解决．
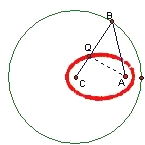
排除法：设动点为Q，
1.当点A在圆内不与圆心C重合，连接CQ并延长，交于圆上一点B，由题意知QB=QA，
又QB+QC=R，所以QA+QC=R，即Q的轨迹为一椭圆；如图。
2.如果是点A在圆C外，由QCR=QA，得QCQA=R，为一定值，即Q的轨迹为双曲线的一支；
3.当点A与圆心C重合，要使QB=QA，则Q必然在与圆C的同心圆，即Q的轨迹为一圆；
则本题选D.
故选D.
练习册系列答案
相关题目
