题目内容
【题目】已知函数![]() (
(![]() 是自然对数的底数).证明:
是自然对数的底数).证明:
(1)![]() 存在唯一的极值点;
存在唯一的极值点;
(2)![]() 有且仅有两个实根,且两个实根互为相反数.
有且仅有两个实根,且两个实根互为相反数.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)要证明![]() 存在唯一的极值点,通常情况下,即证明
存在唯一的极值点,通常情况下,即证明![]() 有唯一解,且在此解左右两边的单调性不一致即可;
有唯一解,且在此解左右两边的单调性不一致即可;
(2)首先借助第(1)问的结论与零点存在定理证明在![]() 只有一个零点,在
只有一个零点,在![]() 只有一个零点,然后令
只有一个零点,然后令![]() 去证明
去证明![]() ,即可得到
,即可得到![]() 的两根互为相反数.
的两根互为相反数.
证明:(1)![]() 的定义域为
的定义域为![]()
![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,
,
所以存在![]() ,使得
,使得![]()
并且当![]() 时
时![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() 是增函数,
是增函数,
即![]() 是
是![]() 唯一的极值点,且是极小值点。
唯一的极值点,且是极小值点。
(2)由(1)得: ![]() 在
在![]() 上是减函数,其中
上是减函数,其中![]() ,
,
又![]()
所以![]() 在
在![]() 只有一个零点,且这个零点在区间
只有一个零点,且这个零点在区间![]() 上,
上,
![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,
,![]() ,
,
所以![]() 在
在![]() 只有一个零点,且这个零点在区间
只有一个零点,且这个零点在区间![]() 上,
上,
所以![]() 仅有两个零点,分别记作
仅有两个零点,分别记作![]()
由于![]() ,
,
所以![]() ,即
,即![]() ,故
,故![]() .
.
![]()
即![]() 也是
也是![]() 的零点,即
的零点,即![]()
所以![]() ,即
,即![]() 的两根互为相反数.
的两根互为相反数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: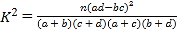 ,其中
,其中![]()