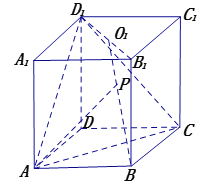
题目内容
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A,B,且
的左焦点为F,短轴的两个端点分别为A,B,且![]() ,
,![]() 为等边三角形.
为等边三角形.

(1)求椭圆C的方程;
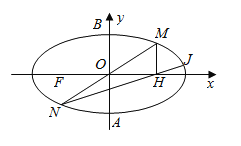
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于P,Q两点,直线
相交于P,Q两点,直线![]() 与椭圆C交于另一点R,求
与椭圆C交于另一点R,求![]() 面积最大值时,直线
面积最大值时,直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)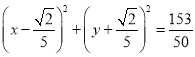 (3)
(3)![]()
【解析】
(1)由题意可得![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,![]() 的关系,可得
的关系,可得![]() 的值,进而得椭圆
的值,进而得椭圆![]() 方程;
方程;
(2)设![]() ,即有
,即有![]() ,
,![]() ,
,![]() ,运用向量的数量积的坐标表示,可得
,运用向量的数量积的坐标表示,可得![]() ,
,![]() ,求出
,求出![]() 的方程,代入椭圆方程,可得
的方程,代入椭圆方程,可得![]() 的坐标,求得
的坐标,求得![]() 的中点坐标和半径,进而可得圆的方程;
的中点坐标和半径,进而可得圆的方程;
(3)设![]() ,代入椭圆方程可得,运用韦达定理和弦长公式,再由三角形的面积公式,运用配方和二次函数的最值得求法,即可得到所求直线的方程.
,代入椭圆方程可得,运用韦达定理和弦长公式,再由三角形的面积公式,运用配方和二次函数的最值得求法,即可得到所求直线的方程.
(1)由题意可得![]() ,即
,即![]() ,又
,又![]() 为等边三角形,可得
为等边三角形,可得![]() ,
,
所以![]() ,
,
所以,椭圆![]() 的方程为:
的方程为:![]() .
.
(2)设![]() ,即有
,即有![]() ,
,![]() ,
,![]() ,
,
由题意得,![]() ,即为
,即为![]() ,解得
,解得![]() ,
,
代入椭圆方程可得,![]() ,解得
,解得![]() ,即有
,即有 ,
,![]() ,
,
所以直线![]() 方程为:
方程为:![]() ,将其代入椭圆方程得:
,将其代入椭圆方程得:![]() ,
,
由![]() ,解得
,解得![]() 点坐标为
点坐标为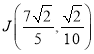 ,则
,则![]() 中点为
中点为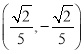 ,
,
所以圆的半径为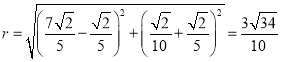 ,
,
即以线段![]() 为直径的圆的方程为:
为直径的圆的方程为: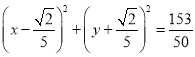 .
.
(3)设![]() ,代入椭圆方程可得,
,代入椭圆方程可得,![]() ,
,
解得![]() ,
,![]() ,则
,则 ,
,
由题意可得直线![]() 的方程为
的方程为![]() ,代入圆的方程
,代入圆的方程![]() 中,
中,
由弦长公式可得 ,
,
则![]() 的面积为
的面积为

令![]() ,即有
,即有![]() ,
,
所以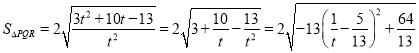
所以当![]() ,即有
,即有![]() ,此时
,此时![]() ,
,![]() 有最大值,
有最大值,
即有直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目