题目内容
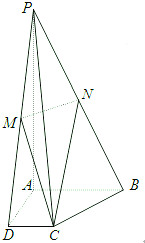
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=
,M,N分别为PD,PB的中点,平面MCN与PA交点为Q.
(Ⅰ)求PQ的长度;
(Ⅱ)求截面MCN与底面ABCD所成二面角的正弦值;
(Ⅲ)求点A到平面MCN的距离.
| 2 |
(Ⅰ)求PQ的长度;
(Ⅱ)求截面MCN与底面ABCD所成二面角的正弦值;
(Ⅲ)求点A到平面MCN的距离.

(本小题满分14分)
(Ⅰ)由题意以A为坐标原点,AD,AB,AP为x,y,z正半轴,
建立空间直角坐标系,
则有:A(0,0,0)、D(
,0,0)、B(0,2,0)、
C(
,1,0)、P(0,0,4)、M(
,0,2)、N(0,1,2).
设Q(0,0,a),由于Q∈平面MCN,
∴存在实数λ,μ,使得
=λ
+μ
,
即(-
,-1,a)=λ(-
,-1,2)+μ(-
,0,2).
由
,得:
.
于是a=2λ+2μ=3,|
|=1.
∴PQ的长度是1.…(5分)
(Ⅱ)设平面MCN的法向量
=(x,y,1),
由
,
取x=
,得
=(
,1,1).
由题意
=(0,0,1)为平面ABCD的法向量.
于是,cos<
,
>=
=
.
∴截面MCN与底面ABCD所成二面角的正弦值为
.…(10分)
(Ⅲ)设点A到平面MCN的距离为d,
∵
=(0,1,2),平面MCN的法向量
=(
,1,1),
∴d=
=
.
∴点A到平面MCN的距离为
.…(14分)
(Ⅰ)由题意以A为坐标原点,AD,AB,AP为x,y,z正半轴,
建立空间直角坐标系,
则有:A(0,0,0)、D(
| 2 |
C(
| 2 |
| ||
| 2 |
设Q(0,0,a),由于Q∈平面MCN,
∴存在实数λ,μ,使得
| CQ |
| CM |
| CN |
即(-
| 2 |
| ||
| 2 |
| 2 |
由
|
|
于是a=2λ+2μ=3,|
| PQ |
∴PQ的长度是1.…(5分)
(Ⅱ)设平面MCN的法向量
| n1 |
由
|
取x=
| 2 |
| n1 |
| 2 |
由题意
| n2 |
于是,cos<
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 2 |
∴截面MCN与底面ABCD所成二面角的正弦值为
| ||
| 2 |
(Ⅲ)设点A到平面MCN的距离为d,
∵
| AN |
| n1 |
| 2 |
∴d=
|
| ||||
|
|
| 3 |
| 2 |
∴点A到平面MCN的距离为
| 3 |
| 2 |

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
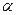 、
、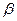 、
、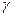 是两两不重合的平面,给出下列命题:①若
是两两不重合的平面,给出下列命题:①若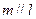 ,
,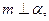 则
则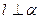 ;②若
;②若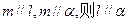 ;③若
;③若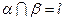 ,
,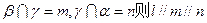 ;④若
;④若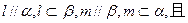 直线l、m为异面直线,则
直线l、m为异面直线,则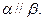 ( )
( )