题目内容
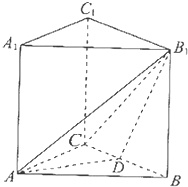
正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.
(1)证明:PQ∥平面DD1C1C;
(2)求线段PQ的长;
(3)求PQ与平面AA1D1D所成的角.
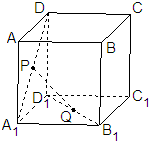
(1)证明:PQ∥平面DD1C1C;
(2)求线段PQ的长;
(3)求PQ与平面AA1D1D所成的角.

(1)证明:如图,
连接A1C1,DC1,则Q为A1C1的中点,
∴PQ∥DC1,且PQ=
DC1,
∴PQ∥平面DD1C1C;
(2)∵正方体ABCD-A1B1C1D1的棱长为1,
∴DC1=
,
∴PQ=
DC1=
;
(3)∵PQ∥DC1,∴PQ、DC1与平面AA1D1D所成的角相等,
∵DC1与平面AA1D1D所成的角为∠C1DD1=45°,
∴PQ与平面AA1D1D所成的角为45°.
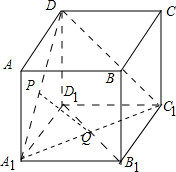
连接A1C1,DC1,则Q为A1C1的中点,
∴PQ∥DC1,且PQ=
| 1 |
| 2 |
∴PQ∥平面DD1C1C;
(2)∵正方体ABCD-A1B1C1D1的棱长为1,
∴DC1=
| 2 |
∴PQ=
| 1 |
| 2 |
| ||
| 2 |
(3)∵PQ∥DC1,∴PQ、DC1与平面AA1D1D所成的角相等,
∵DC1与平面AA1D1D所成的角为∠C1DD1=45°,
∴PQ与平面AA1D1D所成的角为45°.


练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目