题目内容
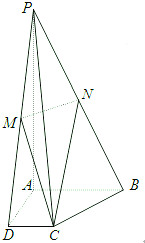
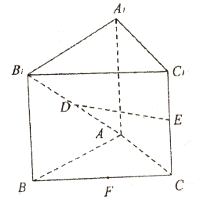
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.
(1)求证:PA∥平面EFG
(2)求三棱锥P-EFG的体积
(3)求点P到平面EFG的距离.

(1)求证:PA∥平面EFG
(2)求三棱锥P-EFG的体积
(3)求点P到平面EFG的距离.

证明:(1)∵E、G分别是PC、BC的中点
∴EG是△PBC的中位线
∴EG∥PB
又∵PB?平面PAB,EG?平面PAB
∴EG∥平面PAB
∵E、F分别是PC、PD的中点
∴EF∥CD
又∵底面ABCD为正方形
∴CD∥AB
∴EF∥AB
又∵AB?平面PAB,EF?平面PAB
∴EF∥平面PAB
又EF∩EG=E
∴平面EFG∥平面PAB
∵PA?平面PAB
∴PA∥平面EFG
(2)∵底面ABCD为正方形
∴GC⊥CD
∵PD⊥平面ABCD
∴GC⊥PD
又∵CD∩PD=D
∴GC⊥平面PCD
∴GC为三棱锥G-PEF的高
∵PD=AB=4
∴S△PEF=
S△PCD=
•
•PD•CD=2
GC=
BC=2
∴VP-EFG=VG-PEF=
×2×2=
(3)取AD的中点M.连接MF并延长,过P作PN⊥MF=N.
∵EF⊥PD,EF⊥AD,PD∩AD=D
∴EF⊥平面PDA,
∵PN?平面PDA,
∴EF⊥PN,
又∵PN⊥MN,MN∩EF=F
∴PN⊥平面FEMG
即PN是点P到平面EFG的距离,
在△PNF中,PF=2,∠PFN=45°
∴PN=
即点P到平面EFG的距离为
.
∴EG是△PBC的中位线
∴EG∥PB
又∵PB?平面PAB,EG?平面PAB
∴EG∥平面PAB
∵E、F分别是PC、PD的中点
∴EF∥CD
又∵底面ABCD为正方形
∴CD∥AB
∴EF∥AB
又∵AB?平面PAB,EF?平面PAB
∴EF∥平面PAB
又EF∩EG=E
∴平面EFG∥平面PAB
∵PA?平面PAB
∴PA∥平面EFG
(2)∵底面ABCD为正方形
∴GC⊥CD
∵PD⊥平面ABCD
∴GC⊥PD
又∵CD∩PD=D
∴GC⊥平面PCD
∴GC为三棱锥G-PEF的高
∵PD=AB=4
∴S△PEF=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |

GC=
| 1 |
| 2 |
∴VP-EFG=VG-PEF=
| 1 |
| 3 |
| 4 |
| 3 |
(3)取AD的中点M.连接MF并延长,过P作PN⊥MF=N.
∵EF⊥PD,EF⊥AD,PD∩AD=D
∴EF⊥平面PDA,
∵PN?平面PDA,
∴EF⊥PN,
又∵PN⊥MN,MN∩EF=F
∴PN⊥平面FEMG
即PN是点P到平面EFG的距离,
在△PNF中,PF=2,∠PFN=45°
∴PN=
| 2 |
即点P到平面EFG的距离为
| 2 |

练习册系列答案
相关题目