题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() ,点
,点![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的倾斜角分别为
的倾斜角分别为![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
【答案】(1)![]() (2)直线
(2)直线![]() 过定点,该定点的坐标为
过定点,该定点的坐标为![]() .
.
【解析】试题分析:(1)由已知得![]() ,
, ![]() ,解方程即可得解;
,解方程即可得解;
(2)设直线MN方程为y=kx+m,与椭圆联立得![]() .设
.设![]() ,
, ![]() ,,由此利用韦达定理结合已知条件能求出直线MN的方程为y=k(x-2),从而能证明直线MN过定点(2,0).
,,由此利用韦达定理结合已知条件能求出直线MN的方程为y=k(x-2),从而能证明直线MN过定点(2,0).
试题解析:
(1)由椭圆![]() 的离心率
的离心率![]() 得
得![]() ,其中
,其中![]() ,
,
∴![]() ,∴
,∴ ![]() 解得
解得![]() ,
, ![]() ,
, ![]() ,
,
∴椭圆的方程为![]() .
.
(2)由题意,知直线![]() 存在斜率,设其方程为
存在斜率,设其方程为![]() .由
.由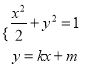
消去![]() ,得
,得![]() .设
.设![]() ,
, ![]() ,
,
则![]() ,
,
即![]() ,
, ![]() ,
, ![]() .
.
且![]()
由已知![]() ,得
,得![]() ,即
,即![]() .
.
化简,得![]()
∴![]() 整理得
整理得![]() .
.
∴直线![]() 的方程为
的方程为![]() ,因此直线
,因此直线![]() 过定点,该定点的坐标为
过定点,该定点的坐标为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】海安市江淮文化园是以江淮历史文化为底蕴的人文景观,整个园区由白龙故里、先贤景区、凤山书院、中国名人艺术馆群四大景区组成.据估计,其中凤山书院景区每天的水电、人工等固定成本为1000元,另每增加一名游客需另外增加成本10元,凤山书院景区门票单价x(元)(x∈N*)与日门票销售量![]() (张)的关系如下表,并保证凤山书院景区每天盈利.
(张)的关系如下表,并保证凤山书院景区每天盈利.
x | 20 | 35 | 40 | 50 |
y | 400 | 250 | 200 | 100 |
(1)在坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定y与x的函数关系式;
的对应点,并确定y与x的函数关系式;
(2)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(3)请写出凤山书院景区的日利润![]() 的表达式,并回答该景区怎样定价才能获最大日利润?
的表达式,并回答该景区怎样定价才能获最大日利润?