Question

【题目】将两块三角板按图甲方式拼好，其中， ， ，

，现将三角板沿折起，使在平面上的射影恰好在上，如图乙．

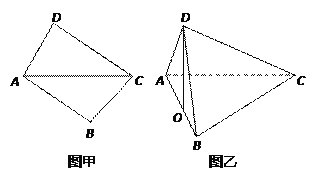
（1）求证： ；

（2）求证： 为线段中点；

（3）求二面角的大小的正弦值．

Answer 1

【答案】（1）见解析（2）见解析（3）

【解析】试题分析：（2）由AD在平面ABC上的射影与BC垂直，即可证明；
（2）通过计算，求得AD=BD，再由等腰三角形高线即中线的性质证得；
（3）利用射影定理作出二面角D-AC-B的平面角，再由正弦定义求得．

试题解析：

(1)证明：由已知D在平面ABC上的射影

O恰好在AB上, ∴DO⊥平面ABC，

∴AO是AD在平面ABC上的射影．

又∵BC⊥AB，∴BC⊥AD．

(2)解：由(1)得AD⊥BC，又AD⊥DC

又BC∩DC=C，∴AD⊥平面BDC

又∵BD平面ADB，∴AD⊥BD，

在RT⊿ABD中，由已知AC = 2，得，AD = 1，∴BD = 1, ∴BD = AD,

∴O是AB的中点.

(3)解：过D作DE⊥AC于E，连结OE，

∵DO⊥平面ABC，∴OE是DE在平面ABC上的射影．∴OE⊥AC

∴∠DEO是二面角D－AC－B的平面角，

且

即二面角D－AC－B的正弦值为．