题目内容
【题目】设函数f(x)=|x﹣2|﹣|2x+l|.
(I)求不等式f(x)≤x的解集;
(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.
【答案】解:(Ⅰ)x≤﹣ ![]() 时,x+3≤x,不成立;
时,x+3≤x,不成立;
﹣ ![]() <x<2时,﹣3x+1≤x,解得x≥
<x<2时,﹣3x+1≤x,解得x≥ ![]() ,∴
,∴ ![]() ≤x<2;
≤x<2;
x≥2时,﹣x﹣3≤x,∴x≥﹣ ![]() ,∴x≥2,
,∴x≥2,
综上所述,不等式f(x)≤x的解集为[ ![]() ,+∞);
,+∞);
(II )x∈[﹣2,﹣1]时,f(x)=x+3,最小值为1.
∵不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,
∴t2﹣t≤1,
∴ ![]() ≤t≤
≤t≤ ![]()
【解析】(Ⅰ)根据绝对值的几何运用,分类讨论,求得f(x)≤x的解集.(Ⅱ)x∈[﹣2,﹣1]时,f(x)=x+3,最小值为1,再根据t2﹣t≤1,求得实数t的取值范围.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 算得,
算得, ![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
【题目】我们为了探究函数![]() 的部分性质,先列表如下:
的部分性质,先列表如下:
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.004 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
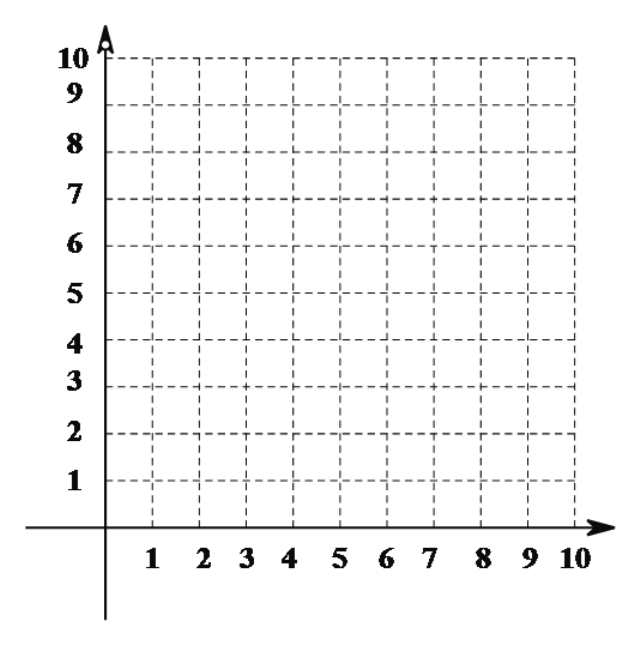
观察表中![]() 值随
值随![]() 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
首先比较容易看得出来:此函数在区间![]() 上是递减的;
上是递减的;
(1)函数![]() 在区间 上递增
在区间 上递增
当![]() 时,
时,![]() = .
= .
(2)请你根据上面性质作出此函数的大概图像;
(3)试用函数单调性的定义证明:函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
