题目内容
9.设实数x,y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≥1\end{array}$,则不等式x2+$\frac{y^2}{2}$≤λ有解的实数λ的最小值为$\frac{1}{3}$.分析 令${x^2}+\frac{y^2}{2}=t\;(t>0)$,把不等式x2+$\frac{y^2}{2}$≤λ有解转化为求x2+$\frac{y^2}{2}$的最小值,由椭圆${x^2}+\frac{y^2}{2}=t$与线段x+y=1(0≤x≤1,0≤y≤1)相切,判别式等于0求得t的值.
解答 解:令${x^2}+\frac{y^2}{2}=t\;(t>0)$,当椭圆${x^2}+\frac{y^2}{2}=t$与线段x+y=1(0≤x≤1,0≤y≤1)相切时,t最小.
如图,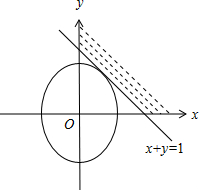
联立$\left\{\begin{array}{l}{x^2}+\frac{y^2}{2}=t\\ x+y=1\end{array}\right.$,消去y得3x2-2x+1-2t=0,
由△=(-2)2-4×3×(1-2t)=0,得$t=\frac{1}{3}$.
即$λ≥\frac{1}{3}$,∴实数λ的最小值为$\frac{1}{3}$.
点评 本题考查了简单的线性规划,考查数学转化思想方法,关键是利用椭圆${x^2}+\frac{y^2}{2}=t$与线段x+y=1(0≤x≤1,0≤y≤1)相切求出x2+$\frac{y^2}{2}$的最小值,是中档题.

练习册系列答案
相关题目
17.如图,在正方体ABCD-A1B1C1D1中,下面结论不正确的是( )
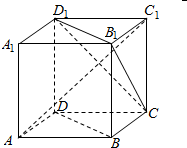

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
14.已知 (1-2i)z=5(i为虚数单位),则复数z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
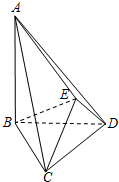 如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.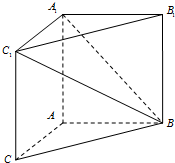 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,