题目内容
1．已知集合A={x|x2-x≤0}，B={-1，0，1}，则A∩B={0，1}．分析 求出集合A，利用集合的基本运算进行求解即可．
解答 解：A={x|x2-x≤0}={x|0≤x≤1}，B={-1，0，1}，
则A∩B={0，1}，
故答案为：{0，1}
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
12．已知顶点为坐标原点O的抛物线C1与双曲线C2：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）都过点M（$\frac{2}{3}$，$\frac{2\sqrt{6}}{3}$），且它们有共同的一个焦点F．则双曲线C2的离心率是（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
16．执行如图所示的程序框图，若a=7．则输出的S=（ ）
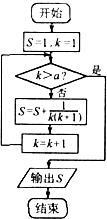
| A． | $\frac{6}{7}$ | B． | $\frac{15}{8}$ | C． | $\frac{13}{7}$ | D． | $\frac{11}{6}$ |
6．某三棱锥的三视图如图所示，则该三棱锥各面中，最小的面积为（ ）
| A． | $\frac{\sqrt{6}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | 1 | D． | $\frac{\sqrt{6}}{4}$ |