题目内容
2.已知数列{an}满足:a1=1,an+1•an-2an+1=0(n∈N*).(Ⅰ)猜测数列{an}的通项公式,并用数学归纳法证明你的结论;
(Ⅱ)设n,k为任意两个正整数,用反证法证明:$\frac{1+{a}_{n}}{{a}_{k}}$与$\frac{1+{a}_{k}}{{a}_{n}}$中至少有一个小于2.
分析 (Ⅰ)先猜想通项公式,利用数学归纳法证明.
(Ⅱ)先假设(Ⅱ)假设$\frac{1+{a}_{n}}{{a}_{n}}≥2$,且$\frac{1+{a}_{k}}{{a}_{n}}≥2$,因为an,ak>0,利用两式子加和后的式子退出与已知矛盾,得出原命题成立.
解答 解:(Ⅰ)由已知,${a}_{n+1}=\frac{2{a}_{n}-1}{{a}_{n}}=2-\frac{1}{{a}_{n}}$,又a1=2,则a2=2-$\frac{1}{2}=\frac{3}{2}$
a3=2-$\frac{2}{3}=\frac{4}{3}$,a4=2-$\frac{3}{4}=\frac{5}{4}$,由此可猜想:${a}_{n}=\frac{n+1}{n}$
证明:(1)当n=1时,${a}_{1}=2=\frac{1+1}{1}$,所以猜想正确.
(2)假设当n=k(k≥1,k∈Z)时,猜想成立,即${a}_{k}=\frac{k+1}{k}$
则${a}_{k+1}=2-\frac{1}{{a}_{k}}=2-\frac{k}{k+1}=\frac{k+2}{k+1}$=$\frac{(k+1)+1}{k+1}$,即当n=k+1时也成立.
结合(1)(2)可知,数列{an}的递推公式是${a}_{n}=\frac{n+1}{n}$
(Ⅱ)假设$\frac{1+{a}_{n}}{{a}_{n}}≥2$,且$\frac{1+{a}_{k}}{{a}_{n}}≥2$,因为an,ak>0
则1+an>2an,且1+ak>2an,两式相加得,(1+an)+(1+ak)≥2an+2ak,即an+ak≤2
因为${a}_{n}=\frac{n+1}{n}=1+\frac{1}{n}>1,{a}_{n}=\frac{k+1}{k}=1+\frac{1}{k}$>1,则:ak+an>2,矛盾.
所以假设不成立,即:$\frac{1+{a}_{n}}{{a}_{k}}$与$\frac{1+{a}_{k}}{{a}_{n}}$中至少有一个小于2.
点评 本题主要考查了数学归纳法和反证法在数列题目中的应用,高考经常涉及,属中档题型.


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
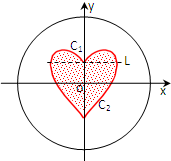 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )| A. | $\frac{1}{4}$-$\frac{1}{18π}$ | B. | $\frac{1}{16}$-$\frac{1}{18π}$ | C. | $\frac{1}{8}$+$\frac{1}{18π}$ | D. | $\frac{1}{8}$+$\frac{36}{35π}$ |
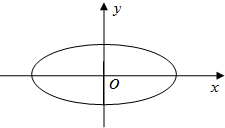 如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.
如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.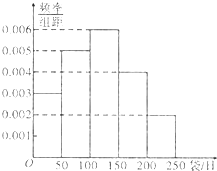 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.
如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.