题目内容
17.如图,在正方体ABCD-A1B1C1D1中,下面结论不正确的是( )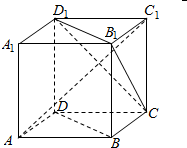
| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
分析 利用正方体侧棱垂直于底面的性质,结合线面平行、线面垂直、面面垂直的判定逐一核对四个选项得答案.
解答  解:对于A,∵ABCD-A1B1C1D1为正方体,∴BD∥B1D1,由线面平行的判定可得BD∥面CB1D1,A正确;
解:对于A,∵ABCD-A1B1C1D1为正方体,∴BD∥B1D1,由线面平行的判定可得BD∥面CB1D1,A正确;
对于B,连接AC,∵ABCD-A1B1C1D1为正方体,∴BD⊥AC,且CC1⊥BD,由线面垂直的判定可得BD⊥面ACC1,∴BD⊥AC1,B正确;
对于C,由上可知BD⊥面ACC1,又BD∥B1D1,∴B1D1⊥面ACC1,则平面ACC1A1⊥CB1D1,C正确;
对于D,异面直线AD与CB1所成的角即为直线BC与CB1所成的角,为45°,D错误.
故选:D.
点评 本题考查命题的真假判断与应用,考查学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
12.已知顶点为坐标原点O的抛物线C1与双曲线C2:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)都过点M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),且它们有共同的一个焦点F.则双曲线C2的离心率是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
6.某三棱锥的三视图如图所示,则该三棱锥各面中,最小的面积为( )


| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{6}}{4}$ |
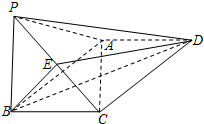 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.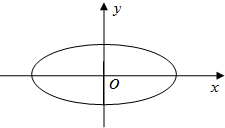 如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.
如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.