题目内容
18.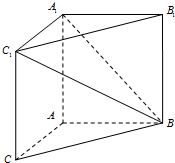 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,(1)求二面角A1-BC1-B1的余弦值;
(2)在线段BC1存在点D,使得AD⊥A1B,求$\frac{BD}{B{C}_{1}}$的值.
分析 (1)建立空间直角坐标系,求出平面A1BC1的法向量、平面BB1C1的法向量,利用向量的夹角公式,即可求二面角A1-BC1-B1的余弦值;
(2)设D(x,y,z)是直线BC1上一点,且$\overrightarrow{BD}=λ\overrightarrow{B{C_1}}$,可得$\overrightarrow{AD}=(4λ,3-3λ,4λ)$,利用AD⊥A1B,即可求$\frac{BD}{B{C}_{1}}$的值.
解答 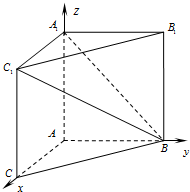 解:(1)如图,以A为原点建立空间直角坐标系A-xyz,
解:(1)如图,以A为原点建立空间直角坐标系A-xyz,
则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
设平面A1BC1的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{{\begin{array}{l}{n•\overrightarrow{{A_1}B}=0}\\{n•\overrightarrow{{A_1}{C_1}}=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{3y-4z=0}\\{\;\;\;4x=0}\end{array}}\right.$,
令z=3,则x=0,y=4,所以$\overrightarrow{n}$=(0,4,3).
同理可得,平面BB1C1的法向量为$\overrightarrow{m}$=(3,4,0),
所以cos<$\overrightarrow{n}$,$\overrightarrow{m}$>=$\frac{16}{25}$.
由题知二面角A1-BC1-B1为锐角,
所以二面角A1-BC1-B1的余弦值为$\frac{16}{25}$.…5分
(2)设D(x,y,z)是直线BC1上一点,且$\overrightarrow{BD}=λ\overrightarrow{B{C_1}}$.
所以(x,y-3,z)=λ(4,-3,4).解得x=4λ,y=3-3λ,z=4λ.
所以$\overrightarrow{AD}=(4λ,3-3λ,4λ)$.
由$\overrightarrow{AD}•\overrightarrow{{A_1}B}=0$,即9-25λ=0.解得$λ=\frac{9}{25}$.
因为$\frac{9}{25}∈[0,1]$,所以在线段BC1上存在点D,使得AD⊥A1B.
此时,$\frac{BD}{{B{C_1}}}=λ=\frac{9}{25}$.…10分.
点评 本题考查二面角的平面角,考查利用空间向量解决数学问题,考查学生分析解决问题的能力,属于中档题.


| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{6}}{4}$ |
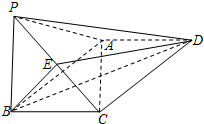 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点. 如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.
如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点. 如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.
如图,BD是四边形ABCD的外接圆⊙O的直径,PA⊥平面ABCD,E为PD的中点,已知∠ABD=∠CBD=60°,PA=BD=2.