题目内容
14.设关于x的不等式|x-2|<a(a∈R)的解集为A,且$\frac{3}{2}$∈A,-$\frac{1}{2}$∉A.(1)对任意的x∈R,|x-1|+|x-3|≥a2+a恒成立,且a∈N,求a的值.
(2)若a+b=1,a,b∈R+,求$\frac{1}{3b}$+$\frac{b}{a}$的最小值,并指出取得最小值时a的值.
分析 (1)由$\frac{3}{2}$∈A,-$\frac{1}{2}$∉A可得$\frac{1}{2}$<a≤$\frac{5}{2}$,再由绝对值不等式的性质可得|x-1|+|x-3|的最小值为2,结合恒成立思想,可得a2+a≤2,解出不等式,求交集,再由a∈N,即可得到a;
(2)由条件可得$\frac{1}{3b}$+$\frac{b}{a}$=$\frac{a+b}{3b}$+$\frac{b}{a}$,运用基本不等式求出最小值,同时求出取等号的a的值.
解答 解:(1)关于x的不等式|x-2|<a(a∈R)的解集为A,且$\frac{3}{2}$∈A,-$\frac{1}{2}$∉A,
则a>|$\frac{3}{2}$-2|且a≤|-$\frac{1}{2}$-2|,即有$\frac{1}{2}$<a≤$\frac{5}{2}$,①
?x∈R,|x-1|+|x-3|≥|(x-1)-(x-3)|=2,即有
|x-1|+|x-3|的最小值为2,
?x∈R,|x-1|+|x-3|≥a2+a恒成立,即有
a2+a≤2,解得-2≤a≤1,②
由①②可得$\frac{1}{2}$<a≤1,
由a∈N,则a=1;
(2)若a+b=1,a>0,b>0,
则$\frac{1}{3b}$+$\frac{b}{a}$=$\frac{a+b}{3b}$+$\frac{b}{a}$=$\frac{1}{3}$+($\frac{a}{3b}$+$\frac{b}{a}$)
≥$\frac{1}{3}$+2$\sqrt{\frac{a}{3b}•\frac{b}{a}}$=$\frac{1+2\sqrt{3}}{3}$,
当且仅当$\frac{a}{3b}$=$\frac{b}{a}$,即a=$\frac{3-\sqrt{3}}{2}$∈($\frac{1}{2}$,$\frac{5}{2}$],b=$\frac{\sqrt{3}-1}{2}$时,
取得最小值,且为$\frac{1+2\sqrt{3}}{3}$.
点评 本题考查绝对值不等式的解法,以及绝对值不等式的性质,考查基本不等式的运用,考查运算能力,属于中档题和易错题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案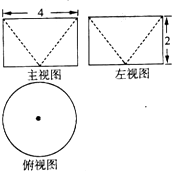 已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1.直径为6的球的体积为V2,则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1.直径为6的球的体积为V2,则V1:V2=( )| A. | 1:2 | B. | 2:27 | C. | 1:3 | D. | 4:27 |
| A. | {x|x<-5或x>-2} | B. | {x|x≤-5或x≥-2} | C. | {x|x≤-3或x≥-1} | D. | {x|x<-3或x>-1} |
 如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )
如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
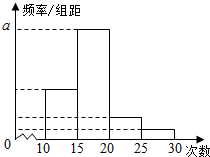 保持口腔卫生不仅对牙齿健康有好处,对预防早老性痴呆症(阿尔茨海默氏症)也是一个十分重要的因素,某市医疗工作人员对某社区人鱼进行了刷牙次数的统计,随机抽取了40人作为样本,得到这40人每月刷牙的次数,根据此数据得到频率分布表和频率分布直方图如下:
保持口腔卫生不仅对牙齿健康有好处,对预防早老性痴呆症(阿尔茨海默氏症)也是一个十分重要的因素,某市医疗工作人员对某社区人鱼进行了刷牙次数的统计,随机抽取了40人作为样本,得到这40人每月刷牙的次数,根据此数据得到频率分布表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 24 | n |
| [20,25) | 4 | P |
| [25,30) | 2 | 0.05 |
| 合计 | 40 | 1 |
(2)若该社区有240人,试估计该社区每月刷牙次数在区间[10,15)内的人数;
(3)在所取样本中,从每月刷牙的次数不少于20次的人员中任选2人,求至多一人每月刷牙次数在区间[25,30)内的概率.