题目内容
11.若等差数列{an}前n项和Sn有最大值,且$\frac{{{a_{11}}}}{{{a_{12}}}}$<-1,则当数列{Sn}的前n项和Tn取最大值时,n的值为( )| A. | 11 | B. | 12 | C. | 22 | D. | 23 |
分析 确定d<0,再由$\frac{{{a_{11}}}}{{{a_{12}}}}<-1$,知a11>0,a12<0,从而有a11+a12>0,即可得出结论.
解答 解:由等差数列的前n项和有最大值,可知d<0,再由$\frac{{{a_{11}}}}{{{a_{12}}}}<-1$,知a11>0,a12<0,从而有a11+a12>0,即S22>0,S23<0,从而使得数列{Sn}的前n项和取最大值的n=22,
故选C.
点评 本小题主要考查对等差数列通项以及变化规律的理解,还包括前n项和的理解,理解了等差数列性质以及特点的学生解决此类问题会比较容易.

练习册系列答案
相关题目
19.直线l过抛物线C:y2=4x的焦点,且与抛物线C交于A、B两点,过点A、B分别向抛物线的准线作垂线,垂足分别为P、Q,则四边形APQB的面积的最小值为( )
| A. | 6 | B. | 8 | C. | $8\sqrt{2}$ | D. | $10\sqrt{2}$ |
6.某城市随机监测一年内100天的空气质量PM2.5的数据API,结果统计如下:
(1)若将API值低于150的天气视为“好天”,并将频率视为概率,根据上述表格,预测今年高考6月7日、8日两天连续出现“好天”的概率;
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出5天,再从这5天中任取3天计算企业利润之和,求利润之和小于80万元的概率.
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出5天,再从这5天中任取3天计算企业利润之和,求利润之和小于80万元的概率.
16. 对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
(1)求出表中M,p及图中a的值;
(2)在所取样本中,从参加社会实践的次数不少于20次的学生中任选3人,记参加社会实践次数在区间[25,30)内的人数为X,求X的分布列和期望.
 对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:| 分组 | 频数 | 频率 |
| [10,15) | 20 | 0.25 |
| [15,20) | 48 | n |
| [20,25) | m | p |
| [25,30) | 4 | 0.05 |
| 合计 | M | 1 |
(2)在所取样本中,从参加社会实践的次数不少于20次的学生中任选3人,记参加社会实践次数在区间[25,30)内的人数为X,求X的分布列和期望.
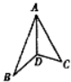 在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°. 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证: