如图.网格纸是由边长为x的小正方形组成.某几何体的三视图如图中粗线所示.已知该几何体的体积为128.则x=( )A．1B．2C．3D．$\frac{3}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

2．

如图，网格纸是由边长为x的小正方形组成，某几何体的三视图如图中粗线所示，已知该几何体的体积为128，则x=（　　）

A．

B．

C．

D．

$\frac{3}{2}$

分析根据三视图得出该几何体四棱锥，利用几何体的性质结合体积公式求解体积即可．

解答解；根据三视图得出该几何体四棱锥，
底面的边长为长和宽为6x，2x，的矩形，
且四棱锥的顶点在底面的射影恰为矩形的边长的三等分点，
四棱锥的高位4x，
∴该几何体的体积为V=$\frac{1}{3}×2x×6x×4x$=128，16x³=128，x=2，
故选：B

点评本题考查了空间几何体的三视图，几何体的体积，学生的空间想象能力，思维能力，属于中档题．

练习册系列答案

13．设A（x₁，y₁），B（x₂，y₂）是函数f（x）=$\frac{1}{2}+{log_2}\frac{x}{1-x}$的图象上任意两点，P是AB中点，且P的横坐标为$\frac{1}{2}$．
（Ⅰ）求证：P点的纵坐标为定值；
（Ⅱ）若S_n=$f（\frac{1}{n}）+f（\frac{2}{n}）+…+f（\frac{n-1}{n}）$，n∈N^*，且n≥2，求S_n．

10．已知命题p：“将函数y=sin（2x+θ）的图象沿x轴向右平移$\frac{π}{16}$个单位后，得到一个关于y轴对称的图象”，命题q“θ=kπ+$\frac{5π}{8}$（k∈Z）“，则p是q的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

17．求$\frac{12+1{6k}^{2}}{16{+k}^{4}+{8k}^{2}}$的最大值．

7．已知函数f（x）=x+1（0≤x≤1），g（x）=2^x-$\frac{1}{2}$（x≥1），函数h（x）=$\left\{\begin{array}{l}{f（x），0≤x＜1}\\{g（x），x≥1}\end{array}\right.$，若方程h（x）-k=0，k∈[$\frac{3}{2}$，2）有两个不同的实根m，n（m＞n≥0），则n•g（m）的取值范围为（　　）

14．设关于x的不等式|x-2|＜a（a∈R）的解集为A，且$\frac{3}{2}$∈A，-$\frac{1}{2}$∉A．
（1）对任意的x∈R，|x-1|+|x-3|≥a²+a恒成立，且a∈N，求a的值．
（2）若a+b=1，a，b∈R⁺，求$\frac{1}{3b}$+$\frac{b}{a}$的最小值，并指出取得最小值时a的值．

11．

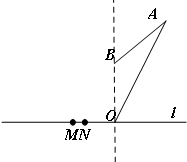如图：我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船，MN=1km，我国海监船在点M的正东方向30km的点O处，观测到一日系船正匀速直线航向我国海域，当该日系船位于点O的北偏东30°方向上的A处（OA=20$\sqrt{3}$km）时，我方开始向日方喊话，但该日系船仍匀速航行，40min后，又测该日系船位于点O的正北方向上的点B处，且OB=20km．（参考数据：$\sqrt{3}$≈1.732）
（1）求该日系船航行的速度．
（2）若该日系船不改变方向继续航行，则其是否会正好行至我国捕鱼船停泊处（即M、N处）？请经过计算说明理由．

19．直线l过抛物线C：y²=4x的焦点，且与抛物线C交于A、B两点，过点A、B分别向抛物线的准线作垂线，垂足分别为P、Q，则四边形APQB的面积的最小值为（　　）

试题分类