题目内容
3.已知函数y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)(1)求函数的最小正周期;
(2)求函数的对称轴、对称中心、单调递增区间.
分析 (1)利用三角函数的周期性及其求法即可得解.
(2)由$\frac{1}{2}$x-$\frac{π}{4}$=k$π+\frac{π}{2}$,k∈Z可解得函数的对称轴;由$\frac{1}{2}$x-$\frac{π}{4}$=kπ,k∈Z可解得对称中心;由2kπ$-\frac{π}{2}$≤$\frac{1}{2}$x-$\frac{π}{4}$≤2k$π+\frac{π}{2}$,k∈Z,可解得单调递增区间.
解答 解:(1)∵y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)
∴函数的最小正周期T=$\frac{2π}{\frac{1}{2}}$=4π.
(2)由$\frac{1}{2}$x-$\frac{π}{4}$=k$π+\frac{π}{2}$,k∈Z可解得函数的对称轴为:x=2kπ+$\frac{3π}{2}$,k∈Z;
由$\frac{1}{2}$x-$\frac{π}{4}$=kπ,k∈Z可解得对称中心是:(2kπ$+\frac{π}{2}$,0),k∈Z;
由2kπ$-\frac{π}{2}$≤$\frac{1}{2}$x-$\frac{π}{4}$≤2k$π+\frac{π}{2}$,k∈Z,可解得单调递增区间是:[4kπ-$\frac{π}{2}$,4kπ+$\frac{3π}{2}$],k∈Z.
点评 本题主要考查了三角函数的周期性及其求法,正弦函数的定义域和值域,正弦函数的单调性及对称性,属于基本知识的考查.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
19.直线l过抛物线C:y2=4x的焦点,且与抛物线C交于A、B两点,过点A、B分别向抛物线的准线作垂线,垂足分别为P、Q,则四边形APQB的面积的最小值为( )
| A. | 6 | B. | 8 | C. | $8\sqrt{2}$ | D. | $10\sqrt{2}$ |
 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)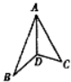 在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°. 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证: