题目内容
18.已知椭圆C的焦点为(-2,0)和(2,0),椭圆上一点到两焦点的距离之和为4$\sqrt{2}$.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=x+m(m∈R)与椭圆C交于A,B两点.当m变化时,求△AOB面积的最大值(O为坐标原点).
分析 (Ⅰ)通过椭圆的定义即得结论;
(Ⅱ)联立直线l与椭圆方程,利用韦达定理、三角形的面积公式、配方法,计算即得结论.
解答 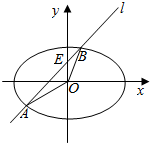 解:(Ⅰ)设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
解:(Ⅰ)设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由题可知:长轴长$2a=4\sqrt{2}$,即$a=2\sqrt{2}$,
半焦距c=2,∴b2=a2-c2=4,
∴椭圆C的标准方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$;
(Ⅱ)联立$\left\{\begin{array}{l}{x^2}+2{y^2}=8\\ y=x+m\end{array}\right.$,消去y并整理得:3x2+4mx+2m2-8=0,
其根的判别式△=(4m)2-4×3×(2m2-8)>0,
解得$-2\sqrt{3}<m<2\sqrt{3}$,
由题意,知m≠0,
设A(x1,y1),B(x2,y2),由韦达定理,
得:${x_1}+{x_2}=-\frac{4m}{3}$,${x_1}{x_2}=\frac{{2{m^2}-8}}{3}$,
设直线l与y轴的交点为E,则E(0,m).
所以△AOB面积$S=\frac{1}{2}•|m|•|{x_1}-{x_2}|$,
${S^2}=\frac{1}{4}{m^2}{({x_1}-{x_2})^2}$
=$\frac{1}{4}{m^2}[{({x_1}+{x_2})^2}-4{x_1}{x_2}]$
=$\frac{1}{4}{m^2}[{(-\frac{4m}{3})^2}-4•\frac{{2{m^2}-8}}{3}]$
=$\frac{2}{9}(-{m^4}+12{m^2})$
=$-\frac{2}{9}{({m^2}-6)^2}+8$(0<m2<12),
∴当m2=6即$m=±\sqrt{6}$时,△AOB面积取得最大值$2\sqrt{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | [$\frac{1}{3}$,$\frac{1}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$] |
| A. | $\frac{4}{3}$ | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
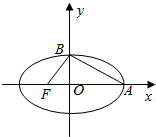 如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.
如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.