题目内容

8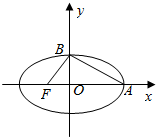．如图所示，椭圆中心在坐标原点，F为左焦点，当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时，该椭圆被称为“黄金椭圆”，其离心率为$\frac{\sqrt{5}-1}{2}$，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$．

分析 由题意可得，FA2=FB2+BA2，把该式转化为关于a，b，c的方程，然后利用c2=b2+a2，可得关于e的二次方程，解出即可

解答 解：由题意可得，FA2=FB2+BA2，即（a+c）2=c2+b2+a2+b2，
整理得b2=ac，
∴c2-a2-ac=0
两边同除以a2，得0=e2-e-1，
∵e＞1
∴e=$\frac{1+\sqrt{5}}{2}$
答案为：$\frac{1+\sqrt{5}}{2}$

点评 本题考查双曲线的简单性质、基本量的求解，属基础题，正确理解新定义是关键．

练习册系列答案
相关题目
18．已知椭圆C的焦点为（-2，0）和（2，0），椭圆上一点到两焦点的距离之和为4$\sqrt{2}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l：y=x+m（m∈R）与椭圆C交于A，B两点．当m变化时，求△AOB面积的最大值（O为坐标原点）．
19．已知点A（3，1）是圆C：（x-m）2+y2=5（m＜3）与椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个公共点，若F1，F2分别是椭圆的左、右焦点，点P（4，4），且直线PF1与圆C相切．
（1）求m的值与椭圆E的方程；
（2）设Q为椭圆E上的一个动点，求$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值范围．
16．过抛物线C：y2=4x上一点P（异于坐标原点O）作直线PA，交抛物线C于点A．
（1）若直线PA过抛物线C的焦点，求$\overrightarrow{OA}$$•\overrightarrow{OP}$的值；
（2）过点P作直线PA的倾斜角互补的直线PB，交抛物线C于点B，设直线AB的斜率k1，抛物线C在点P处的切线斜率为k2，是否存在常数λ，使得k1=λk2？若存在，求λ的值；若不存在，说明理由；
（3）设直线PA过定点（1，0），过点A作与抛物线C在点P处的切线平行的直线l，交抛物线C于点Q，求△APQ面积的最小值．
3．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点与抛物线x2=4$\sqrt{2}$y的焦点重合．F1，F2分别是椭圆C的左右焦点，椭圆的离心率e=$\frac{\sqrt{3}}{3}$．
（1）求椭圆C的方程；
（2）过点F1且斜率为k的直线l与椭圆交于A，B两点，若AF2⊥BF2，求k的值．
13．椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的两个焦点为F1、F2，点P是椭圆上任意一点（非左右顶点），则△PF1F2的周长为（　　）
A．8B．6C．4D．3
20．如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点为A，O为坐标原点，点B在C上，△OBA为等腰直角三角形．
（Ⅰ）求椭圆C的离心率e；
（Ⅱ）若圆x2+y2=1经过C上顶点，与x2+y2=1相切的直线l与C交于不同的两点M，N，求弦|MN|的最大值．
17．已知两个命题p和q，如果p是q的充分不必要条件，那么￢p是￢q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
18．命题p：“a＞1，b＞1”是命题q：“（a-1）（b-1）＞0”（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网