题目内容
【题目】已知f(x)= ![]() ,若函数y=f(x)﹣kx恒有一个零点,则k的取值范围为( )
,若函数y=f(x)﹣kx恒有一个零点,则k的取值范围为( )
A.k≤0
B.k≤0或k≥1
C.k≤0或k≥e
D.k≤0或k≥ ![]()
【答案】B
【解析】解:由y=f(x)﹣kx=0得f(x)=kx,
作出函数f(x)和y=kx的图象如图,
由图象知当k≤0时,函数f(x)和y=kx恒有一个交点,
当x≥0时,函数f(x)=ln(x+1)的导数f′(x)= ![]() ,则f′(0)=1,
,则f′(0)=1,
当x<0时,函数f(x)=ex﹣1的导数f′(x)=ex , 则f′(0)=e0=1,
即当k=1时,y=x是函数f(x)的切线,
则当0<k<1时,函数f(x)和y=kx有3个交点,不满足条件.
当k≥1时,函数f(x)和y=kx有1个交点,满足条件.
综上k的取值范围为k≤0或k≥1,
故选:B.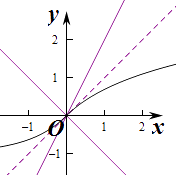

练习册系列答案
相关题目
【题目】甲、乙两个班级共有105名学生,某次数学考试按照“大于等于85分为优秀,85分以下为非优秀”的原则统计成绩后,得到如下![]() 列联表。
列联表。
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知从甲、乙两个班级中随机抽取1名学生,其成绩为优秀的概率为![]() .
.
(1)请完成上面的![]() 列联表;
列联表;
(2)能否有把握认为成绩与班级有关系?