题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,使得
两点,使得![]()
![]() 是椭圆的左焦点
是椭圆的左焦点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1) ![]() (2) 不存在斜率为﹣1直线l与椭圆C相交于M,N两点,使得|F1M|=|F1N|
(2) 不存在斜率为﹣1直线l与椭圆C相交于M,N两点,使得|F1M|=|F1N|
【解析】试题分析:(1)由椭圆的右焦点为![]() ,点
,点 在椭圆
在椭圆![]() 上,列出方程组求出
上,列出方程组求出![]() ,
, ![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的标准方程;(2)假设存在斜率为
的标准方程;(2)假设存在斜率为![]() 直线
直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,使得
两点,使得![]() ,联立方程组,由此利用根的判别式、韦达定理、两点间距离公式、直线斜率公式,结合已知条件推导出不存在斜率为
,联立方程组,由此利用根的判别式、韦达定理、两点间距离公式、直线斜率公式,结合已知条件推导出不存在斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,使得
两点,使得![]() .
.
试题解析:(1)∵椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,点
,点 在椭圆
在椭圆![]() 上,∴
上,∴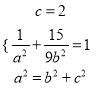 ,解得
,解得![]() ,∴椭圆
,∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)不存在斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,使得
两点,使得![]() ,理由如下:假设存在斜率为
,理由如下:假设存在斜率为![]() 直线
直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,使得
两点,使得![]() ,联立
,联立 ,消除
,消除![]() ,得:
,得: ![]() ,
, ![]() ,解得
,解得![]() ,(*)
,(*)![]() ,
, ![]() ,
, ![]() ,∵
,∵![]() ,
, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,整理,得
,整理,得![]() ,∴
,∴![]() ,∴直线
,∴直线![]() 的斜率:
的斜率: ![]() ,解得
,解得![]() ,不满足(*)式,∴不存在斜率为
,不满足(*)式,∴不存在斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,使得
两点,使得![]() .
.

练习册系列答案
相关题目



