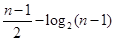题目内容
已知 分别是函数
分别是函数
的两个极值点,且 ,
, ,则
,则 的取值范围是( )
的取值范围是( )
 分别是函数
分别是函数
的两个极值点,且
 ,
, ,则
,则 的取值范围是( )
的取值范围是( )A.   | B. | C. | D. |
D
解:∵函数f(x)="1" /3 x3+1/ 2 ax2+2bx
∴f′(x)=x2+ax+2b
又∵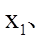 ∈(0,1),
∈(0,1),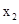 ∈(1,2),
∈(1,2),
∴ f′(0)=2b>0
f′(1)=1+a+2b<0
f′(2)=4+2a+2b>0 其对应的平面区域如下图所示:
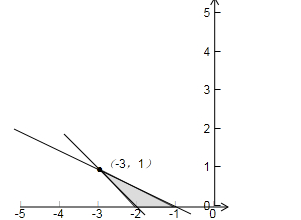
由图可得:当x=-3,y=1时,b-2 /a-1 取最小值1/ 4 ;
当x=-1,y=0时,b-2 /a-1 取最大值1;
∴f′(x)=x2+ax+2b
又∵
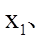 ∈(0,1),
∈(0,1),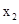 ∈(1,2),
∈(1,2),∴ f′(0)=2b>0
f′(1)=1+a+2b<0
f′(2)=4+2a+2b>0 其对应的平面区域如下图所示:

由图可得:当x=-3,y=1时,b-2 /a-1 取最小值1/ 4 ;
当x=-1,y=0时,b-2 /a-1 取最大值1;

练习册系列答案
相关题目
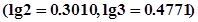
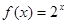
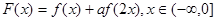 的最大值;
的最大值;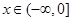 ,使
,使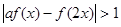 成立,试求
成立,试求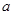 的取值范围;
的取值范围;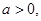 且
且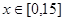 时,不等式
时,不等式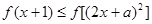 恒成立,求
恒成立,求 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.
 ,项数为31项的等差数列
,项数为31项的等差数列 满足
满足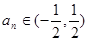 ,且公差
,且公差 ,若
,若 ,当
,当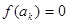 时
时 =( )
=( ) ,则一个符合条件的函数表达式为______
,则一个符合条件的函数表达式为______ 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 .
. 是偶函数;
是偶函数; 在
在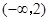 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; ,②
,② ,③
,③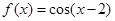 ,
, ,定义
,定义 ,其中,
,其中, ,则
,则 ( )
( )