题目内容
16.在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1的极坐标方程为ρ(cosθ+sinθ)=-2,曲线C2的参数方程为$\left\{\begin{array}{l}{x=t^2}\\{y=2\sqrt{2}t}\end{array}\right.$ (t为参数),则C1与C2交点的直角坐标为(2,-4).分析 曲线C1的极坐标方程为ρ(cosθ+sinθ)=-2,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得直角坐标方程.曲线C2的参数方程为$\left\{\begin{array}{l}{x=t^2}\\{y=2\sqrt{2}t}\end{array}\right.$ (t为参数),化为普通方程:y2=8x.联立解出即可.
解答 解:曲线C1的极坐标方程为ρ(cosθ+sinθ)=-2,化为直角坐标方程:x+y+2=0.
曲线C2的参数方程为$\left\{\begin{array}{l}{x=t^2}\\{y=2\sqrt{2}t}\end{array}\right.$ (t为参数),化为普通方程:y2=8x.
联立$\left\{\begin{array}{l}{x+y+2=0}\\{{y}^{2}=8x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$,
则C1与C2交点的直角坐标为(2,-4).
故答案为:(2,-4).
点评 本题考查了极坐标化为直角坐标方程、参数方程化为普通方程、曲线的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左右焦点分别为F1,F2,过F2作双曲线C的一条渐近线的垂线,垂足为H,若△HF1F2的面积为a2,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
7.某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(Ⅰ)从该班随机选1名同学,求该同学至少参加一个社团的概率;
(Ⅱ)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
| 参加书法社团 | 未参加书法社团 | |
| 参加演讲社团 | 8 | 5 |
| 未参加演讲社团 | 2 | 30 |
(Ⅱ)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
4.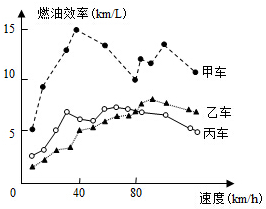 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )| A. | 消耗1升汽油,乙车最多可行驶5千米 | |
| B. | 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 | |
| C. | 甲车以80千米/小时的速度行驶1小时,消耗10升汽油 | |
| D. | 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 |
11.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为( )
| A. | 0.4 | B. | 0.6 | C. | 0.8 | D. | 1 |
1.执行如图所示的程序框图,输出的k值为( )
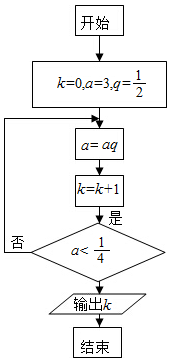

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |

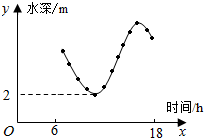 如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为( )