题目内容
16.已知偶函数f(x),当x∈[0,2)时,f(x)=2sinx,当x∈[2,+∞)时,f(x)=log2x,则$f({-\frac{π}{3}})+f(4)$=( )| A. | $\sqrt{3}+2$ | B. | 1 | C. | 3 | D. | $-\sqrt{3}+2$ |
分析 函数f(x)为偶函数,可得f(-$\frac{π}{3}$)=f($\frac{π}{3}$)再将其代入f(x)=2sinx,进行求解,再根据x∈[2,+∞)时f,f(x)=log2x,求出f(4),从而进行求解.
解答 解:∵函数f(x)为偶函数,
∴f(-$\frac{π}{3}$)=f($\frac{π}{3}$)
∵当x∈[0,2)时f(x)=2sinx,
∴f(x)=2sin$\frac{π}{3}$=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$;
∵当x∈[2,+∞)时f(x)=log2x,
∴f(4)=log24=2,
∴$f({-\frac{π}{3}})+f(4)$=2+$\sqrt{3}$,
故选:A
点评 此题主要考查函数值的求解问题,解题的过程中需要注意函数的定义域,是一道基础题

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.设集合S=$\left\{{x|\frac{1}{2}<{2^x}<8}\right\}$,T={x|x<a或x>a+2},S∪T=R,则a的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
1.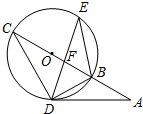 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
下列结论中,错误的是( )
 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的下列结论中,错误的是( )
| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
16.若函数f(x)在R上可导,且f(x)>f′(x),则当a>b时,下列不等式成立的是( )
| A. | eaf(a)>ebf(b) | B. | ebf(a)>eaf(b) | C. | ebf(b)>eaf(a) | D. | eaf(b)>ebf(a) |