题目内容
6．利用诱导公式计算$\frac{cos（-45°）cos30°tan585°}{tan（-120°）}$．分析 运用诱导公式及特殊角的三角函数值即可化简求值
解答 解：$\frac{cos（-45°）cos30°tan585°}{tan（-120°）}$=$\frac{cos45°cos30°tan45°}{-cot60°}$=$\frac{\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}×1}{-\frac{\sqrt{3}}{3}}$=-$\frac{3\sqrt{2}}{4}$．
点评 本题主要考查了诱导公式及特殊角的三角函数值的应用，属于基本知识的考查．
练习册系列答案
口算题天天练系列答案
相关题目
14．
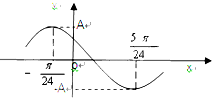已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如下图所示，且直线y=A与曲线y=f（x）（-$\frac{π}{24}$$≤x≤\frac{11π}{24}$）所围成的封闭图形的面积为π，则f（$\frac{π}{8}$）+f（$\frac{2π}{8}$）+f（$\frac{3π}{8}$）+…+f（$\frac{2015π}{8}）$的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如下图所示，且直线y=A与曲线y=f（x）（-$\frac{π}{24}$$≤x≤\frac{11π}{24}$）所围成的封闭图形的面积为π，则f（$\frac{π}{8}$）+f（$\frac{2π}{8}$）+f（$\frac{3π}{8}$）+…+f（$\frac{2015π}{8}）$的值为（ ）| A． | -$\sqrt{3}$ | B． | -1-$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | -1+$\sqrt{3}$ |
1．过顶点在原点，焦点在y轴正半轴的抛物线的焦点F作直线l交抛物线于A、B两点，过点A、B分别作抛物线准线的垂线，垂足分别为点C、D，|AF|=2|BF|，且$\overrightarrow{DC}$•$\overrightarrow{BA}$=72，则该抛物线方程为（ ）
| A． | x2=8y | B． | x2=10y | C． | x2=9y | D． | x2=5y |
18．已知x、y满足约束条件$\left\{\begin{array}{l}x+y-1≤0\\ x-y≤0\\ x≥0\end{array}\right.$则 z=x+2y 的最大值为（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
16．已知偶函数f（x），当x∈[0，2）时，f（x）=2sinx，当x∈[2，+∞）时，f（x）=log2x，则$f（{-\frac{π}{3}}）+f（4）$=（ ）
| A． | $\sqrt{3}+2$ | B． | 1 | C． | 3 | D． | $-\sqrt{3}+2$ |