题目内容
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为 ![]() ,则该产品投放市场第几天的销售额最高?最高为多少千元?
,则该产品投放市场第几天的销售额最高?最高为多少千元?
【答案】解:(Ⅰ)根据题意知,当1≤x≤40时,一次函数y=ax+b过点A(4,23),b(32,20), 代入函数求得a= ![]() ,b=22;
,b=22;
当40<x≤100时,一次函数y=ax+b过点C(60,22),B(90,7),
代入函数求得a=﹣ ![]() ,b=52
,b=52
∴f(x)= 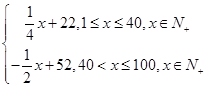
(Ⅱ)设日销售额为S(x),则当1≤x≤40时,S(x)=f(x)g(x)=﹣ ![]() (x2﹣21x﹣9592),
(x2﹣21x﹣9592),
当x=10或11时,[S(x)]max=808.5(千元),
当40<x≤100时,S(x)=f(x)g(x)=﹣ ![]() ,
,
当x=41时,[S(x)]max=714(千元)
∵714<808.5,
∴日销售额最高是在第10天或第11天,最高值为808.5千元.
【解析】(Ⅰ)价格直线上升,直线下降,说明价格函数f(x)是一次函数,由表中对应关系用待定系数法易求f(x)的表达式;(Ⅱ)由销售额=销售量×时间,得日销售额函数S(x)的解析式,从而求出S(x)的最大值.

【题目】某网站对“爱飞客”飞行大会的日关注量x(万人)与日点赞量y(万次)进行了统计对比,得到表格如下:
x | 3 | 5 | 6 | 7 | 9 |
y | 2 | 3 | 3 | 4 | 5 |
由散点图象知,可以用回归直线方程 ![]() 来近似刻画它们之间的关系.
来近似刻画它们之间的关系.
(Ⅰ)求出y关于x的回归直线方程,并预测日关注量为10万人时的日点赞量;
(Ⅱ)一个三口之家参加“爱飞客”亲子游戏,游戏规定:三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球,大人摸出每个红球得奖金10元,小孩摸出1个红球得奖金50元.求该三口之家所得奖金总额不低于50元的概率.
参考公式:b= 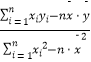 ; 参考数据:
; 参考数据: ![]() =200,
=200, ![]() =112.
=112.