题目内容
【题目】(理科答)已知数列{an}及等差数列{bn},若a1=3,an= ![]() an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
(1)证明数列{an﹣2}为等比数列;
(2)求数列{an}及数列{bn}的通项公式;
(3)设数列{anbn}的前n项和为Tn , 求Tn .
【答案】
(1)证明:a1=3,an= ![]() an﹣1+1(n≥2),
an﹣1+1(n≥2),
an﹣2= ![]() (an﹣1﹣2),
(an﹣1﹣2),
则数列{an﹣2}为首项为1,公比为 ![]() 的等比数列
的等比数列
(2)解:(由(1)可得an﹣2=( ![]() )n﹣1,
)n﹣1,
即为an=2+( ![]() )n﹣1,
)n﹣1,
a1=b2=3,
2a3+a2=b4=2(2+ ![]() )+2+
)+2+ ![]() =7,
=7,
可得等差数列{bn}的公差d= ![]() =2,
=2,
则bn=b2+(n﹣2)d=3+2(n﹣2)=2n﹣1
(3)证明:数列{anbn}的前n项和为Tn,
anbn=[2+( ![]() )n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)(
)n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)( ![]() )n﹣1,
)n﹣1,
设Sn=1( ![]() )0+3(
)0+3( ![]() )+5(
)+5( ![]() )2+…+(2n﹣1)(
)2+…+(2n﹣1)( ![]() )n﹣1,
)n﹣1,
![]() Sn=1(
Sn=1( ![]() )+3(
)+3( ![]() )2+5(
)2+5( ![]() )3+…+(2n﹣1)(
)3+…+(2n﹣1)( ![]() )n,
)n,
相减可得, ![]() Sn=1+2[(
Sn=1+2[( ![]() )+(
)+( ![]() )2+(
)2+( ![]() )3+…+(
)3+…+( ![]() )n﹣1]﹣(2n﹣1)(
)n﹣1]﹣(2n﹣1)( ![]() )n
)n
=1+2[ 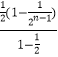 ]﹣(2n﹣1)(
]﹣(2n﹣1)( ![]() )n,
)n,
化简可得Sn=6﹣ ![]() ,
,
则Tn=2 ![]() n(1+2n﹣1)+6﹣
n(1+2n﹣1)+6﹣ ![]() =2n2+6﹣
=2n2+6﹣ ![]()
【解析】(1)an= ![]() an﹣1+1的两边减2,再由等比数列的定义即可得证;(2)运用等比数列和等差数列的通项公式,计算即可得到;(3)求得anbn=[2+(
an﹣1+1的两边减2,再由等比数列的定义即可得证;(2)运用等比数列和等差数列的通项公式,计算即可得到;(3)求得anbn=[2+( ![]() )n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)(
)n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)( ![]() )n﹣1 , 再由数列的求和方法:分组求和和错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
)n﹣1 , 再由数列的求和方法:分组求和和错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为 ![]() ,则该产品投放市场第几天的销售额最高?最高为多少千元?
,则该产品投放市场第几天的销售额最高?最高为多少千元?
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.