Question

【题目】已知函数f（x）=ax﹣lnx（a∈R）．
（1）当a=1时，求f（x）的最小值；
（2）若存在x∈[1，3]，使 +lnx=2成立，求a的取值范围；
（3）若对任意的x∈[1，+∞），有f（x）≥f（ ）成立，求a的取值范围．

Answer 1

【答案】
（1）解：f（x）=x﹣lnx（x＞0）的导数为f′（x）=1﹣ = ，

当x＞1时，f′（x）＞0，f（x）递增；当0＜x＜1时，f′（x）＞0，f（x）递减．

即有f（x）在x=1处取得极小值，也为最小值，且为1

（2）解：存在x∈[1，3]，使 +lnx=2成立，

即为 =2﹣lnx，

即有a= ，

设g（x）= ，x∈[1，3]，

则g′（x）=（1﹣lnx）（1+ ），

当1＜x＜e时，g′（x）＞0，g（x）递增；当e＜x＜3时，g′（x）＜0，g（x）递减．

则g（x）在x=e处取得极大值，且为最大值e+ ；

g（1）=2，g（3）=3（2﹣ln3）+ ＞2，

则a的取值范围是[2，e+ ]

（3）解：若对任意的x∈[1，+∞），有f（x）≥f（ ）成立，

即为ax﹣lnx≥ ﹣ln ，

即有a（x﹣ ）≥2lnx，x≥1，

令F（x）=a（x﹣ ）﹣2lnx，x≥1，

F′（x）=a（1+ ）﹣ ，

当x=1时，原不等式显然成立；

当x＞1时，由题意可得F′（x）≥0在（1，+∞）恒成立，

即有a（1+ ）﹣ ≥0，

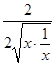即a≥ ，由 = ＜ =1，

则a≥1．

综上可得a的取值范围是[1，+∞）

【解析】（1）求得f（x）的导数，求得单调区间，可得f（x）的极小值，也为最小值；（2）由题意可得a= ，设g（x）= ，x∈[1，3]，求出导数和单调区间，极值和最值，即可得到所求a的范围；（3）由题意可得ax﹣lnx≥ ﹣ln ，即有a（x﹣ ）≥2lnx，x≥1，令F（x）=a（x﹣ ）﹣2lnx，x≥1，求出导数，讨论x=1，x＞1时，F（x）递增，运用分离参数和基本不等式，即可得到a的范围．