题目内容
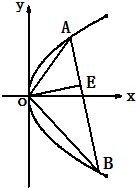
已知不过坐标原点O的直线L与抛物线y2=2x相交于A、B两点,且OA⊥OB,OE⊥AB于E.
①求证:直线L过定点;
②求点E的轨迹方程.
①求证:直线L过定点;
②求点E的轨迹方程.

①令直线ty=x-b(b≠0)与抛物线y2=2x相交于A(x1,y1)、B(x2,y2)两点(给直线方程给分)…(1分)
由
得:y2-2ty-2b=0…(2分)
于是,y1、y2是此方程的两实根,由韦达定理得:y1+y2=2ty1y2=-2b…(3分)
x1x2=(ty1+b)(ty2+b)=t2y1y2+tb(y1+y2)+b2=b2…(4分)
又OA⊥OB?x1x2+y1y2=0…(5分)
∴b2-2b=0,又b≠0,
∴b=2…(6分)
故直线L:ty=x-2过定点C(2,0)…(8分)
②∵O(0,0),C(2,0),OE⊥CE…(9分)
∴点E的轨迹是以线段OC为直径的圆除去点O,…(11分)
故点E的轨迹方程为(x-1)2+y2=1(x≠0)…(12分)
说明:直线L的方程设为y=kx+b又没有讨论k不存在的情况扣(2分);轨迹方程中没有限制x≠0扣(1分).
由
|
于是,y1、y2是此方程的两实根,由韦达定理得:y1+y2=2ty1y2=-2b…(3分)
x1x2=(ty1+b)(ty2+b)=t2y1y2+tb(y1+y2)+b2=b2…(4分)
又OA⊥OB?x1x2+y1y2=0…(5分)
∴b2-2b=0,又b≠0,
∴b=2…(6分)
故直线L:ty=x-2过定点C(2,0)…(8分)
②∵O(0,0),C(2,0),OE⊥CE…(9分)
∴点E的轨迹是以线段OC为直径的圆除去点O,…(11分)
故点E的轨迹方程为(x-1)2+y2=1(x≠0)…(12分)
说明:直线L的方程设为y=kx+b又没有讨论k不存在的情况扣(2分);轨迹方程中没有限制x≠0扣(1分).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
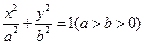 的左焦点为F,上顶点为A,直线
的左焦点为F,上顶点为A,直线 AF的倾斜角为
AF的倾斜角为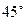 (1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线
(1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线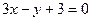 相切,求椭圆的方程及圆M的方程
相切,求椭圆的方程及圆M的方程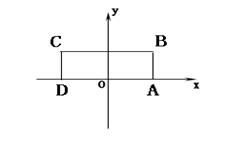
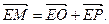 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;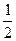 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且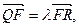 求实数
求实数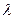 的取值范围.
的取值范围.