题目内容
椭圆
+y2=1的弦被点(
,
)平分,则这条弦所在的直线方程是______.
| x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设这条弦的两端点为A(x1,y1),B(x2,y2),斜率为k,
则
,
两式相减再变形得
+k(y1+y2)=0,
又弦中点为(
,
),
故k=-
,
故这条弦所在的直线方程y-
=-
(x-
),整理得2x+4y-3=0.
故答案为:2x+4y-3=0.
则
|
两式相减再变形得
| x1+x2 |
| 2 |
又弦中点为(
| 1 |
| 2 |
| 1 |
| 2 |
故k=-
| 1 |
| 2 |
故这条弦所在的直线方程y-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2x+4y-3=0.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
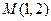 ,它们在
,它们在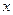 轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .
轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .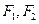 为椭圆
为椭圆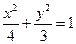 左、右焦点,过椭圆中心任作一条直线与椭圆交于
左、右焦点,过椭圆中心任作一条直线与椭圆交于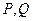 两点,当四边形
两点,当四边形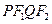 面积最大时,
面积最大时,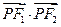 的值等于 .
的值等于 .