题目内容
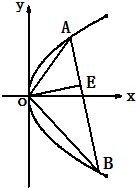
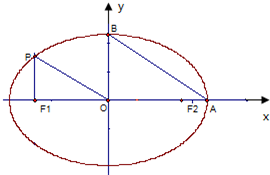
如图,从椭圆E:
+
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,|F1A|=
+
,
(1)求椭圆E的方程.
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点C,D,且
⊥
?若存在,写出该圆的方程,并求|CD|的取值范围;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 5 |
(1)求椭圆E的方程.
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点C,D,且
| OC |
| OD |

(1)由题意可求点P的坐标为(-c,
),由AB∥OP得,
∴a=
,b=
,
椭圆E的方程为
+
=1;
(2)假设存符合题意的圆,切线与椭圆的交点为C(x1,y1),D(x2,y2),
当该圆的切线不垂直x轴时,设其方程为y=kx+m,
由方程组
,得x2+2(kx+m)2=10,即(1+2k2)x2+4kmx+2m2-10=0,
则△=16k2m2-4(1+2k2)(2m2-10)=8(10k2-m2+5)>0,即10k2-m2+5>0,
,
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
-
+m2=
,
要使
⊥
,需使x1x2+y1y2=0,即
+
=0,
∴3m2-10k2-10=0,∴k2=
≥0,
又10k2-m2+5>0,∴
,
∴m2≥
,即m≥
或m≤-
,
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴圆的半径为r=
,r2=
=
=
,
所求的圆为x2+y2=
,
此时圆的切线y=kx+m都满足m≥
或m≤-
;
而当切线的斜率不存在时,切线为x=±
,与椭圆
+
=1的两个交点为(
,±
)或(-
,±
),满足
⊥
;
综上所述,存在圆心在原点的圆x2+y2=
,使得该圆的任意一条切线与椭圆E恒有两个交点C,D,且
⊥
.
∵
,
∴(x1-x2)2=(x1+x2)2-4x1x2=(-
)2-4×
=
,
∴|CD|=
|x1-x2|=
=
=
,
①当k≠0时,|CD|=
,
∵4k2+
+4≥8,∴0<
≤
,
∴
<
[1+
]≤15,
∴
| b2 |
| a |
|
∴a=
| 10 |
| 5 |
椭圆E的方程为
| x2 |
| 10 |
| y2 |
| 5 |
(2)假设存符合题意的圆,切线与椭圆的交点为C(x1,y1),D(x2,y2),
当该圆的切线不垂直x轴时,设其方程为y=kx+m,
由方程组
|
则△=16k2m2-4(1+2k2)(2m2-10)=8(10k2-m2+5)>0,即10k2-m2+5>0,
|
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
| k2(2m2-10) |
| 1+2k2 |
| 4k2m2 |
| 1+2k2 |
| m2-10k2 |
| 1+2k2 |
要使
| OC |
| OD |
| 2m2-10 |
| 1+2k2 |
| m2-10k2 |
| 1+2k2 |
∴3m2-10k2-10=0,∴k2=
| 3m2-10 |
| 10 |
又10k2-m2+5>0,∴
|
∴m2≥
| 10 |
| 3 |
| ||
| 3 |
| ||
| 3 |
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴圆的半径为r=
| |m| | ||
|
| m2 |
| 1+k2 |
| m2 | ||
1+
|
| 10 |
| 3 |
所求的圆为x2+y2=
| 10 |
| 3 |
此时圆的切线y=kx+m都满足m≥
| ||
| 3 |
| ||
| 3 |
而当切线的斜率不存在时,切线为x=±
| ||
| 3 |
| x2 |
| 10 |
| y2 |
| 5 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| OC |
| OD |
综上所述,存在圆心在原点的圆x2+y2=
| 10 |
| 3 |
| OC |
| OD |
∵
|
∴(x1-x2)2=(x1+x2)2-4x1x2=(-
| 4km |
| 1+2k2 |
| 2m2-10 |
| 1+2k2 |
| 8(10k2-m2+5) |
| (1+2k2)2 |
∴|CD|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
|
|
①当k≠0时,|CD|=
|
∵4k2+
| 1 |
| k2 |
| 1 | ||
4k2+
|
| 1 |
| 8 |
∴
| 40 |
| 3 |
| 40 |
| 3 |
| 1 | ||
4k2+
|
∴
2
|