题目内容
(本题满分15分)设椭圆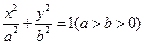 的左焦点为F,上顶点为A,直线
的左焦点为F,上顶点为A,直线 AF的倾斜角为
AF的倾斜角为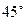 (1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线
(1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线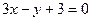 相切,求椭圆的方程及圆M的方程
相切,求椭圆的方程及圆M的方程
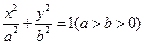 的左焦点为F,上顶点为A,直线
的左焦点为F,上顶点为A,直线 AF的倾斜角为
AF的倾斜角为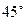 (1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线
(1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线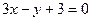 相切,求椭圆的方程及圆M的方程
相切,求椭圆的方程及圆M的方程(Ⅰ)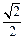 (Ⅱ)
(Ⅱ) 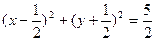
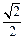 (Ⅱ)
(Ⅱ) 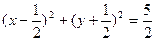
⑴因为直线AF的倾斜角为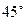 ,所以
,所以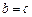 , 2分所以椭圆的离心率为
, 2分所以椭圆的离心率为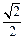 .…4分
.…4分
⑵由⑴知 ,……5分直线
,……5分直线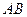 的方程为
的方程为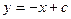 ,右准线方程为
,右准线方程为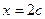 7分可得
7分可得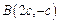 ,…8分又
,…8分又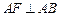 ,所以过
,所以过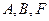 三点的圆的圆心坐标为
三点的圆的圆心坐标为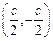 ,…9分
,…9分
半径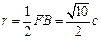 ,10分因为过
,10分因为过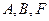 三点的圆恰好与直线
三点的圆恰好与直线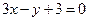 相切,所以圆心到直线
相切,所以圆心到直线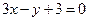 的距离等于半径
的距离等于半径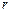 ,即
,即 ,……12分得
,……12分得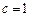 ,……13分
,……13分
所以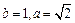 ,所以椭圆的方程为
,所以椭圆的方程为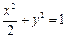 .14分
.14分
圆M的方 程为
程为 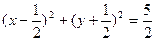 ……15分
……15分
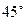 ,所以
,所以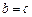 , 2分所以椭圆的离心率为
, 2分所以椭圆的离心率为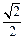 .…4分
.…4分⑵由⑴知
 ,……5分直线
,……5分直线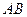 的方程为
的方程为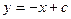 ,右准线方程为
,右准线方程为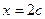 7分可得
7分可得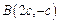 ,…8分又
,…8分又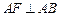 ,所以过
,所以过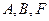 三点的圆的圆心坐标为
三点的圆的圆心坐标为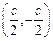 ,…9分
,…9分半径
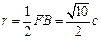 ,10分因为过
,10分因为过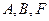 三点的圆恰好与直线
三点的圆恰好与直线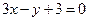 相切,所以圆心到直线
相切,所以圆心到直线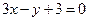 的距离等于半径
的距离等于半径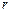 ,即
,即 ,……12分得
,……12分得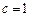 ,……13分
,……13分所以
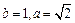 ,所以椭圆的方程为
,所以椭圆的方程为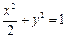 .14分
.14分圆M的方
 程为
程为 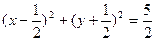 ……15分
……15分
练习册系列答案
相关题目
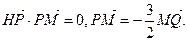
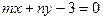 与圆
与圆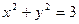 没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆
没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆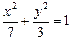 的公共点有_________个。
的公共点有_________个。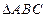 中,
中,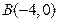 ,
,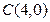 ,
,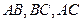 成等差数列,求点
成等差数列,求点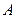 的轨迹。
的轨迹。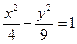 上的两个动点,满足
上的两个动点,满足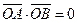 。(Ⅰ)求证:
。(Ⅰ)求证: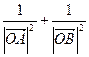 为定值; (Ⅱ)动点P在线段AB上,满足
为定值; (Ⅱ)动点P在线段AB上,满足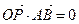 ,求证:点P在定圆上.
,求证:点P在定圆上.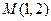 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .
轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .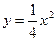 的焦点,离心率
的焦点,离心率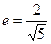 。(1)求椭圆的标准方程
。(1)求椭圆的标准方程 ;(2)过椭圆C的右焦点
;(2)过椭圆C的右焦点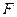 作直线
作直线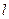 交椭圆C于A、B两点,交y轴于M,若
交椭圆C于A、B两点,交y轴于M,若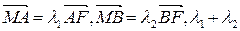 为定值吗?证明你的结论。
为定值吗?证明你的结论。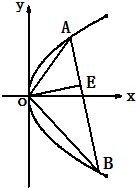
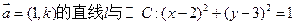 ,相交于M、N两点.
,相交于M、N两点.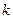 的取值范围;
的取值范围; 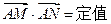 ;
;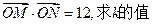 .
.