题目内容
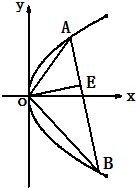
长方形ABCD,AB=2
,BC=1,以AB的中点O为原点建立如图所示的平面直角坐标系.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程:
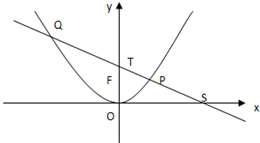
(2)过点p(0,2)的直线m与(1)中椭圆只有一个公共点,求直线m的方程:
(3)过点p(0,2)的直线l交(1)中椭圆与M,N两点,是否存在直线l,使得以弦MN为直径的圆恰好过原点?若存在,直线l的方程;若不存在,说明理由.

| 2 |
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程:
(2)过点p(0,2)的直线m与(1)中椭圆只有一个公共点,求直线m的方程:
(3)过点p(0,2)的直线l交(1)中椭圆与M,N两点,是否存在直线l,使得以弦MN为直径的圆恰好过原点?若存在,直线l的方程;若不存在,说明理由.

(1)由题意可得点A,B,C的坐标分别为(-
,0),(
,0),(
,1).
设椭圆的标准方程是
+
=1(a>b>0).
则2a=AC+BC,
即2a=
+1=4>2
,所以a=2.
所以b2=a2-c2=4-2=2.
所以椭圆的标准方程是
+
=1.
(2)设直线m的方程为y=kx+2,
由
,得(2k2+1)x2+8kx+4=0,
∵直线m与椭圆只有一个公共点,
∴△=64k2-16(k2+1)=0,解得k=±
.
∴直线m的方程为y=
x,或y=-
x.
(3)由题意知,直线l的斜率存在,可设直线l的方程为y=kx+2.
由
,得(1+2k2)x2+8kx+4=0.
因为M,N在椭圆上,
所以△=64k2-16(1+2k2)>0.
设M,N两点坐标分别为(x1,y1),(x2,y2).
则x1+x2=-
,x1x2=
,
若以MN为直径的圆恰好过原点,则
⊥
,
所以x1x2+y1y2=0,
所以,x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0,
所以,
-
+4=0,即
=0,
得k2=2,k=±
.
经验证,此时△=48>0.
所以直线l的方程为y=
x+2,或y=-
x+2.
即所求直线存在,其方程为y=
x+2,或y=-
x+2.
| 2 |
| 2 |
| 2 |
设椭圆的标准方程是
| x2 |
| a2 |
| y2 |
| b2 |
则2a=AC+BC,
即2a=
(2
|
| 2 |
所以b2=a2-c2=4-2=2.
所以椭圆的标准方程是
| x2 |
| 4 |
| y2 |
| 2 |
(2)设直线m的方程为y=kx+2,
由
|
∵直线m与椭圆只有一个公共点,
∴△=64k2-16(k2+1)=0,解得k=±
| ||
| 3 |
∴直线m的方程为y=
| ||
| 3 |
| ||
| 3 |
(3)由题意知,直线l的斜率存在,可设直线l的方程为y=kx+2.
由
|
因为M,N在椭圆上,
所以△=64k2-16(1+2k2)>0.
设M,N两点坐标分别为(x1,y1),(x2,y2).
则x1+x2=-
| 8k |
| 1+2k2 |
| 4 |
| 1+2k2 |
若以MN为直径的圆恰好过原点,则
| OM |
| ON |
所以x1x2+y1y2=0,
所以,x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0,
所以,
| 4(1+k2) |
| 1+2k2 |
| 16k2 |
| 1+2k2 |
| 8-4k2 |
| 1+2k2 |
得k2=2,k=±
| 2 |
经验证,此时△=48>0.
所以直线l的方程为y=
| 2 |
| 2 |
即所求直线存在,其方程为y=
| 2 |
| 2 |

练习册系列答案
相关题目
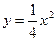 的焦点,离心率
的焦点,离心率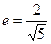 。(1)求椭圆的标准方程
。(1)求椭圆的标准方程 ;(2)过椭圆C的右焦点
;(2)过椭圆C的右焦点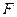 作直线
作直线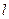 交椭圆C于A、B两点,交y轴于M,若
交椭圆C于A、B两点,交y轴于M,若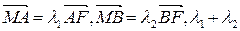 为定值吗?证明你的结论。
为定值吗?证明你的结论。